wspolrzedne srodka odcinka. melania.: oblicz wspolrzedne punktu S przeciecia srodkowych w trojkacie ABC, jesli: A(0,0) B(9,0) C(0,6)

mały miś:: S jest środkiem ciężkości trójkąta S( x_S, y_S)

	xA+xB+xC		yA+yB+yC
xS=		oraz yS=
	3		3

( średnia arytmetyczna współrzędnych wierzchołków trójkąta)

	9		6
xS=		=3 oraz yS=		= 2
	3		3

S( 3,2)

melania.: ale dlaczego to jest srednia arytmetyczna?

mały miś:: Możesz sobie ten wzór wyprowadzić środkowe dzielą się w skali 2:1 licząc od wierzchołków ..

melania.: dalej nie rozumiem.

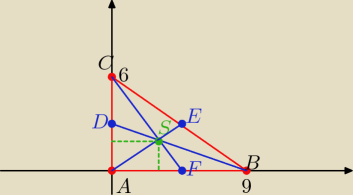
mały miś:: no to tak D( 0,3) −− bo jest środkiem boku AC F( 4,5 ; 0) jest środkiem boku AB piszemy równanie środkowych BD i CF i rozwiązując układ tych równań otrzymasz punkt S środkowa BD: y= ax+ b D( 0,3) i B( 9,0) otrzymasz BD: y= −¹₃x +3 środkowa CF: y= ax+b C( 0,6) F( 4,5:0) otrzymasz: CF: y= ²₃x układ równań: y= −¹₃x +3 i y= ²₃x ²₃x= −¹₃x +3 x= 3 to y= ²₃*3= 2 S( 3,2)

mały miś:: Wyprowadzam wzór , o którym mowa w pierwszym wpisie ( korzystam z rys podanego wyżej) środkowe dzielą się w stosunku 2: 1 licząc od wierzchołka) → → DS = ¹₃ DB

	xa+xC		yA+y+C
D(		,		)
	2		2

→

	xA+xC		YA+yB
DS= [ xS −		, yS −		]
	2		2

→

	xA+xB		yA+yB
DB=[ xB −		, yB−		]
	2		2

→

	1		xB		xA+xB		yB		yA+yB
		DB= [		−		,		−		]
	3		3		6		3		6

	xA+xB		xB		xA+xB
to: xS −		=		−
	2		3		6

	2xB −xA−xB +3xA+3xB
xS=
	6

	2xA+2xB +2xC
xS=
	6

	xA+xB+xC
xS=
	3

i podobnie:

	yA+yB+yC
yS=
	3

zatem:

	xA+xB+xC		yA+yB+yC
S(		,		)
	3		3

c.n.u. Wzór jest bardzo łatwy do zapamiętania .