5 zadań z tożsamości trygonometrycznej chosen:

	ctg α
1. Udowodnij, że: cos2α =
	tg α + ctg α

2. Dany jest ctg α = 5. Oblicz 2sin²α − 3cos²α

	2
3. Mając cos α =		oblicz tg α + sin α
	5

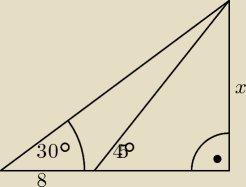
4. Drzewo rzuca cień o długości 15 m a kąt padania promieni wynosi 18^o Oblicz h drzewa. 5. Oblicz x ( z rysunku na górze )

Amaz: 1. wymnoż stronami przez tgx+ctgx dostaniesz:

	cos3x
cosxsinx +		=ctgx teraz stronami mnożysz przez sinx
	sinx

cosxsin²x + cos³x=cosx, dzielisz stronami przez cosx sin²x + cos²x=1, Zgadza się

Amaz: to może zrobie jeszcze podpunkt numer 5 Widzę, że ten mniejszy trójkąt jest równoramienny, więc druga przyprostokątna całego, dużego trójkąta to x+8, zatem:

	x
tg30o=
	x+8

Z tego wynika, że x=4(1+√3), o ile nie pomyliłem się w obliczeniach

chosen: Dziękuję Ci bardzo