calki Justysia89: ∫cos² x dx

Jack: spróbuj przez części f(x)=cosx f'(x)=−sinx g'(x)=cosx g(x)=sinx zauważ, że sin²x=1−cos²x Potem przerzuć całką cos²x na drugą stronę i podziel przez 2 (bo będą 2∫cos²x dx )

Justysia89: dalej niewiem jak to zrobic mozesz mi to rozpisac mam jeszcze 2 przyklad ∫2^3x+8 dx

Jack: kurcze musze iść zrób normalne całkowanie przez części. Potem jak będziesz miała całkę z cos²x zamień wyrażenie pod całką na 1−sin²x. Będziesz miała po jednej stronie ∫cos²xdx a po drugiej coś takiego sinxcosx + x +c−∫cos²xdx. Teraz przerzuć tą całkę na drugą stronę, będziesz miała 2* ∫cos²xdx=sinxcosx +x +c. Teraz wystarczy przez dwa podzielić i dostaniesz czemu równa jest całką z cos²x. w drugim weź 2⁸ przed całkę a w całkę rozwiaż przez podstawienie t=3x.

Jack: sorry, odwrotnie − jak "jak będziesz miała całkę z sin²x, to zamień wyrażenie pod całką (sin²x) na 1−cos²x"

Justysia89: dobra dzieki wielkie moze teraz zaczaje jak cos to do jutra o tej samej porze

AS:

	ax
∫axdx =		przy zał.że a > 0 i a ≠ 1
	ln(a)

Podstawienie:

	1
3*x + 8 = t ⇒3*dx = dt ⇒ dx =		*dt
	3

	1		1		2t		23x + 8
∫23x + 8dx = ∫2t*		*dt =		*		=		+ C
	3		3		ln(2)		3*ln(2)

Amaz: http://www.wolframalpha.com/input/?i=integral+cos^2xdx

Amaz: tam jest "show steps" i można sobie zobaczyć jak tą całkę w krokach wyliczyć

Justysia89: całka oznaczona ²₀∫ x√4−x²dx dzieki za to forum

Jack: podstawienie zrób 4−x²=t Dalej już prosto (tak na oko, "prosto").

Justysia89: A wiesz może jak zrobić to ? Obliczyć pole obszaru zawarte między krzywymi o równaniach: y=9^x x=−1 ; x=1/2 y=0

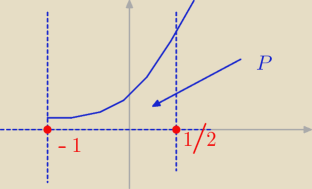
Jack: Policz całkę ∫₋₁^1/2 9^x dx. Chyba proste...

Justysia89: ratujesz mi życie dzieki

Justysia89: a mozesz mi jeszcze w jednym pomóc ? y=2^x y=3^x x=−1 x=1

Jack: miło, że tak wiele można uczynić, robiąc tak niewiele

Jack: Twoje życie już ocalone − spróbuj sama coś zaproponować

Justysia89: jak tego nie napiszesz to moje zycie nie bedzie ocalone

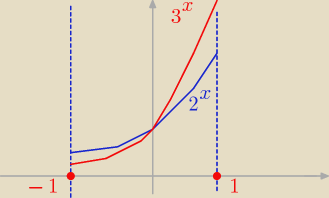
Jack: Trzeba policzyć dwie całki: 1. ∫₋₁⁰ 2^x−3^x dx −− bo 2^x jest NAD 3^x w tym przedziale 2.∫₀¹ 3^x−2^x dx −− bo 3^x jest NAD 2^x w tym przedziale A na koniec dodać do siebie.

Justysia89: dzieki wielkie masz u mnie

Jack:

Basia: P.S. Można się nie przejmować tym "co wyżej" a "co niżej" i napisać, że P=| ∫.........|

Jack: faktycznie

Jack: dokładnie to tak: P= |∫.... | + |∫.... |.

Basia: oczywiście, chodziło mi o jeden obszar