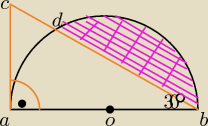
Pole wycinka koła Kiejstut: W trójkącie prostokątnym ABC dane są |AC| = 3cm, |∡CAB| = 90*, |∡ABC| = 30*. Przyprostokątna AB jest średnicą półkola, jak na rysunku. Punkt D jest punktem przecięcia się półokręgu z bokiem BC. Oblicz: a) długość cięciwy |DB| b) pole odcinka koła, zaznaczonego na rysunku

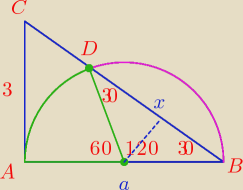
Jack: połącz punkt "o" z punktem "d", powstanie trójkąt równoramienny o kącie rozwartym 120^o, potem skorzsystaj ze wzoru na pole wycinka mając dany promień i kąt rozwarcia. Długość |DB| można policzyć z trojkąta który nam powstanie mając dany promień oraz kąt 30^o (z funkcji tryg,).

Godzio:

	3
tg30 =
	a

	9
a =		= 3√3
	√3

	1
R =		a = 1,5√3
	2

	1   x 2
cos30 =
	1,5√3

√3
	* 1,5√3 * 2 = x
2

x = 4,5

	h
sin30 =
	1,5√3

h = 0,75√3

	1
Pwycinka =		Pkoła − Pm. trójkąta − Pwyc zielonego =
	2

1		4,5 * 0,75√3		1
	π * (1,5√3)2 −		−		π(1,5√3)2 =
2		2		6

3,3375π − 1,6875√3 − 1,125π = 5,55π − 1,6875√3 sprawdź czy się nigdzie nie pomyliłem

Kiejstut: skąd wiemy że ∡DOB ma 120o to dlatego że ∡ACB opiera się na takim samym łuku?

Kiejstut: aha dzięki, nie odświeżyłem

Karolina :): na końcu wkradł ci się błąd a mianowicie : Pwycinka = 1/2 Pkoła − Pm. trójkąta − Pwyc zielonego = 3,375 π − ^27√3₁₆ − ^9π₈\= ^27π₈ − ^27√3₁₆ − ^9π₈\= ^{36π − 27√3}₁₆ = ^9(4−3√3)₁₆

Janek191: Do Godzia : Trzeba było obliczyć pole odcinka koła O − środek koła P_o = P_w − P_ΔBDO

	1		1		1
Pw =		π R2 =		π *( 1,5 √3)2 =		π*2,25*3 =2,25 π
	3		3		3

	1		1
PΔDBO =		R2 * sin 120o =		( 1,5 √3)2 *sin 60o =
	2		2

	1		√3
=		*2,25*3 *		= 1,6875 √3
	2		2

zatem P_o = 2,25 π − 1,6875 √3 ======================== P_o − pole odcinka koła ( zakreskowanego ) P_w − pole wycinka koła o kącie środkowym mającym miarę 120^o.