w trójkacie ABO przeciw prostokatna ABO p{5} czy jesli podziele p{10} Ania: Dany jest trójkat ABO, gdzie A(−2,0), B (0,1), O(0,0). trójkąt prostokątny CDE ma przeciwprostokątna długosci √10 i jest podobny do trójkata ABO. Oblicz obwód i pole trójkata CDE

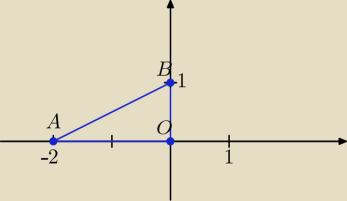
Eta: IABI = √2²+1²= √5 −−− dł. przeciwprostokątnej ΔABO ICDI= √10 ponieważ Δ ABC ~` ΔCDE to skala podobieństwa

	√10		√5*√2
k=		=		= √2
	√5		√5

to:

	Ob(Δ CDE)
		= k = √2
	Ob(ΔABO

	P(ΔCDE)
		= k2= (√2)2= 2
	P(ΔABO)

	2*1
PΔ(ABO)=		= 1
	2

to PΔ(CDE)= 1*k²= 1*2= 2 [j²] Ob(ΔABO)= 2+1+√5= 3+√5 to: Ob(ΔCDE)= k*(3+√5= √2(3+√5)= 3√2+ √10 [j] Wymiary trójkąta ABO; 2, 1, √5 Wymiary trójkąta CDE: 2*k=2√2, 1*k=√2, √5*k=√10