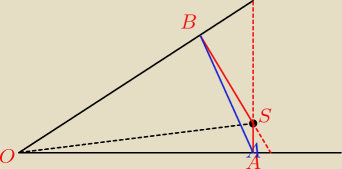
 przedłużyłam, ale nie widzę co ma mi to dać (to nie znaczy, że się tak nie da, po prostu ja nie
widzę) więc może tak:
∡ASB=120
z tw.cosinusów liczę |AB|
AB2=12+42−2*1*4*cos120=1+16+4=21
|AB|=√21
∡SAB=α
∡ABS=β
przedłużyłam, ale nie widzę co ma mi to dać (to nie znaczy, że się tak nie da, po prostu ja nie
widzę) więc może tak:
∡ASB=120
z tw.cosinusów liczę |AB|
AB2=12+42−2*1*4*cos120=1+16+4=21
|AB|=√21
∡SAB=α
∡ABS=β
| sinα | sinβ | sin120 | |||
= | = | ||||
| BS | AS | AB |
| sinα | sinβ | √3 | 1 | ||||
= | = | = | |||||
| 4 | 1 | 2√21 | 2√7 |
| 4 | 2 | |||
sinα= | = | |||
| 2√7 | 2√7 |
| 1 | ||
sinβ= | ||
| 2√7 |
| 1 | 27 | 9*3 | ||||
cos2β=1− | = | = | ||||
| 4*7 | 28 | 4*7 |
| 3√3 | ||
cosβ= | ||
| 2√7 |
| sin60 | sin∡OAB | sin∡OBA | |||
= | = | ||||
| AB | OB | OA |
| sin60 | sin(90−β) | ||
= | |||
| AB | OA |
| √3 | √21*3√3 | |||
OA* | = | |||
| 2 | 2√7 |
| 3√21 | ||
OA= | =3√3 | |
| √7 |
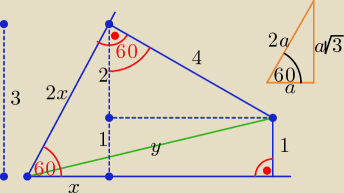 Dzień dobry.
Korzystając z własności trójkąta prostokątnego, którego miary kątów wewnętrznych są
równe 60o i 30o po wprowadzeniu oznaczeń, jak na rysunku, otrzymujemy:
x√3 = 3 ⇒ x = √3 i 2x = 2√3, (2x)2 = 12
Z twierdzenia Pitagorasa: y = √ 12 + 14 = √28 = 2√7
Łatwe zadanie, prawda?
Dzień dobry.
Korzystając z własności trójkąta prostokątnego, którego miary kątów wewnętrznych są
równe 60o i 30o po wprowadzeniu oznaczeń, jak na rysunku, otrzymujemy:
x√3 = 3 ⇒ x = √3 i 2x = 2√3, (2x)2 = 12
Z twierdzenia Pitagorasa: y = √ 12 + 14 = √28 = 2√7
Łatwe zadanie, prawda?


