proszę o rozwiązanie
alucha: zad 1. rozwiąż nierówność |x−1|≤1+|2x+4|
zad 2. rozwiąż równanie (x−√2)2=(x+√2)(x+√2)−x
zad3. określ liczbę rozwiązań równania m2(x−1)+3m=mx−m2 w zależności od wartości parametru m. w
przypadku istnienia rozwiązania wyznacz je.
zad 4. określ wzór funkicji liniowej f której wykres jest nachylony do osi OX pod kątem α=3/4π,
oraz f(−1)=7
a)wyznacz wzór funkcji liniowej g, której wykres jest prostopadły do wykresu funkcji f a jej
miejscem zerowym jest 2
27 maj 20:28
R.W.16l:
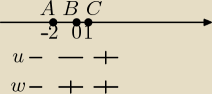
1. |x−1|−2|x+2|≤1
|x−1| − u, x
0=1
|x+2| − w, x
0=−2
z rys. mamy 3 przexziały oraz znaki, jakie odpowiadaja wyrażaniu dla danego przedziału
nazwałem te przedziały A,B,C
A − oba opuszczamy | | z ujemnym znakiem
/1−x−2(−x−2) −> x+5
\x∊(−
∞;−2)
lub ( \/ )
B − jeden op. z uj. znakiem, drugi bez (u z ujemnym)
/1−x−2x−4 −> −3x−3
\x∊<−2;1)
\/
C − oba bez zmian
/x−1−2x−4 −> −x−5
\x∊<1;+
∞)
rysujesz wykres:
|x+5, x∊(−
∞;−2)
f(x)=|−3x−3, x∊<−2;1)
|−x−5, x∊<1;+
∞)
oraz wykres funkcji g(x)=1 i patrzysz dla jakich x wykres f(x) jest ≤ g(x) i odp, jest tten
zbiór
27 maj 20:40
R.W.16l: 4. α=3/4π, oraz f(−1)=7
a wyznaczamy z tego kąta wiedząc, że a=tgα
na wykresie funckji tgx wyszukujesz wartości odpowiadajacej x=3/4pi,
widze, ze to będzie −1, czyli a=−1
dalej f(−1)=7
czyli 7=−1a+b i a=−1
7=1+b
b=6
f: y=−x+6
| | 1 | |
a) prostopadły, czyli jak f: y=a1x+b1, g: y=a2x+b2, to a1*a2=−1, czyli a2=− |
| |
| | a1 | |
a
2=1
czyli g: y=x+d
jeżeli f(2)=0
to 0=2a
2+d
d=−2
g: y=x−2
27 maj 20:46
R.W.16l: Parametry, ehh
nie ma rozwiązan gdy a=0 i b≠0
czyli:
m
2(x−1)+3m=mx−m
2
m
2x−mx−m
2+3m−m
2=0
x(m
2−m)−2m
2+3m=0
m
2−m=0 i −2m
2+3m≠0
m(m−1)=0 i m(−2m+3)≠0
| | 3 | |
(m=0 lub m=1) i m≠0 i m≠ |
| |
| | 2 | |
z tego wychodzi, że dla m=1 nie ma rozwiazań
| | −b | |
Ma dokłądnie jedno rozwiązanie gdy a≠0 i b∊R, postaci x= |
| |
| | a | |
m
2−m≠0 i m∊R
m≠0 i m≠1 i m∊R, czyli m ma dokł jedno rozwiązanie dla dowolnego m∊R−{0;1}
Ma nieskończenie rozw. gdy a=0 i b=0
(m=0 lub m=−1) i −2m
2+3m=0
(m=0 lub m=−1) i m(−2m+3)=0
| | 3 | |
(m=0 lub m=−1) i (m=0 lub m= |
| ) |
| | 2 | |
27 maj 20:55
R.W.16l: (x−√2)2=(x+√2)(x+√2)−x
(x−√2)2−(x+√2)2−x=0
(x−√2−x−√2)(x−√2+x+√2)−x=0
(−2√2)(2x)−x=0
−4√2x−x=0
x(−4√2−1)=0
x=0 lub (−4√2−1)=0
x=0 i x∊R
na koniec
x=0
27 maj 20:59
alucha: dzięki
27 maj 21:18
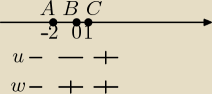 1. |x−1|−2|x+2|≤1
|x−1| − u, x0=1
|x+2| − w, x0=−2
z rys. mamy 3 przexziały oraz znaki, jakie odpowiadaja wyrażaniu dla danego przedziału
nazwałem te przedziały A,B,C
A − oba opuszczamy | | z ujemnym znakiem
/1−x−2(−x−2) −> x+5
\x∊(−∞;−2)
lub ( \/ )
B − jeden op. z uj. znakiem, drugi bez (u z ujemnym)
/1−x−2x−4 −> −3x−3
\x∊<−2;1)
\/
C − oba bez zmian
/x−1−2x−4 −> −x−5
\x∊<1;+∞)
rysujesz wykres:
|x+5, x∊(−∞;−2)
f(x)=|−3x−3, x∊<−2;1)
|−x−5, x∊<1;+∞)
oraz wykres funkcji g(x)=1 i patrzysz dla jakich x wykres f(x) jest ≤ g(x) i odp, jest tten
zbiór
1. |x−1|−2|x+2|≤1
|x−1| − u, x0=1
|x+2| − w, x0=−2
z rys. mamy 3 przexziały oraz znaki, jakie odpowiadaja wyrażaniu dla danego przedziału
nazwałem te przedziały A,B,C
A − oba opuszczamy | | z ujemnym znakiem
/1−x−2(−x−2) −> x+5
\x∊(−∞;−2)
lub ( \/ )
B − jeden op. z uj. znakiem, drugi bez (u z ujemnym)
/1−x−2x−4 −> −3x−3
\x∊<−2;1)
\/
C − oba bez zmian
/x−1−2x−4 −> −x−5
\x∊<1;+∞)
rysujesz wykres:
|x+5, x∊(−∞;−2)
f(x)=|−3x−3, x∊<−2;1)
|−x−5, x∊<1;+∞)
oraz wykres funkcji g(x)=1 i patrzysz dla jakich x wykres f(x) jest ≤ g(x) i odp, jest tten
zbiór