pomocy!!!!!!!!!!!!!!!!!!!!!! Hania =): Podstawą graniastosłupa prostego jest równoległobok o obwodzie 18cm. Przekątne graniastosłupa mają długość 9cm i √33cm, a krawędź boczna ma długość 4 cm. Oblicz objętość graniastosłupa

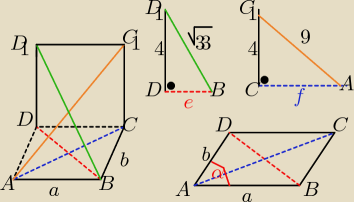
Eta: e, f −−− dł. przekątnych równoległoboku wyznaczamy je z trójkątów prostokatnych DBD₁ i CAC₁ z tw. Pitagorasa e= √17 f= √65 z treści zad. 2a+2b= 18 => a+b= 9 => a= 9−b , b€(0,9) zachodzi związek w równoległoboku: 2a²+2b²= e² +f² ( wykaż to sobie z tw. cosinusów) czyli: 2a²+2b²= 17+65= 82 to: a²+b² = 41 i a= 9 − b rozwiązując ten układ otrzymasz: a= 5 b= 4 P_p= a*b*sinα z tw. cosinusów w ΔABD:

	a2+b2−e2		3
cosα=		= ....... =
	2ab		5

	4
to sinα= √1−cos2α= ....... =
	5

P_p = a*b*sinα= ......... =16 V= P_p*H = 16*4= 64 cm³

Hania =): możesz mi rozwiązać ten układ

Hania =): i policzyć a2+b2−e2 3 cosα= = ....... = 2ab 5 4 to sinα= √1−cos2α= ....... = 5

Eta: a²+b²= 41 i a= 9−b (9−b)²+b²= 41 2b² −18b +81 −41=0 b² −9b +20=0 Δ= 1 √Δ= 1 b= 5 v b= 4 to a= 9−5=4 v a= 9−4=5

	25+16−17		24		3
cosα=		=		=
	2*5*4		5*8		5

	4
sinα= √1−cos2α= √1−925= √1625=
	5

to: P_p= a*b*sinα= 5*4*⁴₅= 16 V=......... 64 cm³