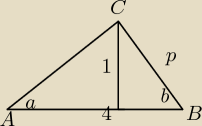
 mam takie zadanie
mam takie zadanie
| sinalfa | cos alfa | |||
Na podstawie rysunku oblicz | + | |||
| cosbeta | ctg2alfa |

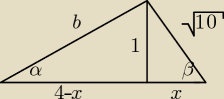 √102=x2+12 → x2=9 → x=±3
b2=(4−x)2+12 → b2=17−8x+x2 → b2=17−24+9=√2 ⇔ b2=(4−3)2+12 = √2
√102=x2+12 → x2=9 → x=±3
b2=(4−x)2+12 → b2=17−8x+x2 → b2=17−24+9=√2 ⇔ b2=(4−3)2+12 = √2
|
| ||||||||||||||||||||
+ | = | ||||||||||||||||||||
|
|
| 1 | √10 | 1 | 1 | √10 | 1 | |||||||
* | + | * | = | + | ||||||||
| √2 | 3 | √2 | 9 | 3√2 | 9√2 |
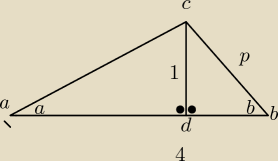 z tw. pitagorasa obliczam odcinek IDBI
12 + DB2= √102
db = 3
obliczam odcinek ad
ad = 4 − db
ad= 4 −3 =1
z tw. pitagorasa obliczam odcinek ac
ac2= 12 + 12
ac=√2
sina =1\ √2
cosb=3\√10
cosa= 1\√2
tga=1
z tw. pitagorasa obliczam odcinek IDBI
12 + DB2= √102
db = 3
obliczam odcinek ad
ad = 4 − db
ad= 4 −3 =1
z tw. pitagorasa obliczam odcinek ac
ac2= 12 + 12
ac=√2
sina =1\ √2
cosb=3\√10
cosa= 1\√2
tga=1