W ostrosłupie prawidłowym czworokątnym dana jest krawędź boczna ostrosłupa równa
Mateuszek: W ostrosłupie prawidłowym czworokątnym dana jest krawędź boczna ostrosłupa równa 18cm i kąt
jaki tworzy ta krawędź z płaszczyzną podstawy ALFA = 60 stopni. Wyznacz pole powierzchni
całkowitej i objętość.
No i tak:
Obleciałem po wzorach, wyprowadziłem je, sporządziłem rysunek i...
http://img84.imageshack.us/i/zdjcie003j.jpg/
... zawisłem. Nie wiem od czego zacząć.
26 maj 08:08
taa:
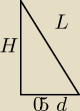
Przepraszam za nieczytelny rysunek

Jak wiadomo podstawą jest kwadrat, więc d= a
√2 czyli 1/2d=
a√22 będziesz mógł wtedy
wyznaczyć a z sinusów, tak samo z wysokością

26 maj 09:00
taa: Do końca rozwiązać czy takie wytłumaczenie wystarczy?
26 maj 09:01
Mateuszek: Prosiłbym o rozwiązanie, bo sam to zrobię, ale chcę sprawdzić, czy mój tok rozumowania pokrywa
się z prawdą.

26 maj 09:09
mila: kat=60 jest pomiędzy przekątna podstawy a krawędzia boczną z tablic odczytasz,ze sin60=p{3]/2
sin60=H/L to H=sin60*L
H=√3/2*18cm
H=9*√3
połowa przekątnej =1/2d to bok trójkata prostokątnego czyli liczysz albo z Pitagorasa albo z
funkcji trygonometrycznych
H2=(1/2d)2=L2
(1/2d)=l82−(9√32=324−81*3=324−243=81
1/2d=√81=9
d=18
d jest przeciwprostokatną trójkąta o bokach a i a czyli d2= a2+a2
d2=2a2
d=√2a2 d=√2a
18=√2a a=18/√2 a=18*√2 /p[2]*√2 mnożac pozbywamy sie pierwiastka z mianownika
a=9√2 dalej podstawdo wzorów na objętość i pole
26 maj 15:25
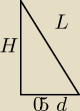 Przepraszam za nieczytelny rysunek
Przepraszam za nieczytelny rysunek  Jak wiadomo podstawą jest kwadrat, więc d= a√2 czyli 1/2d= a√22 będziesz mógł wtedy
wyznaczyć a z sinusów, tak samo z wysokością
Jak wiadomo podstawą jest kwadrat, więc d= a√2 czyli 1/2d= a√22 będziesz mógł wtedy
wyznaczyć a z sinusów, tak samo z wysokością 
