Pola trójkątów Kaaasia: Baaardzo proszę o pomoc Niech P będzie dowolnym punktem wewnętrznym trójkąta ABC. Wykaż, że

x		y		z
	+		+		= 1
h1		h2		h3

gdzie x,y,z oznaczają odległości tego punktu od boków trójkąta, a h1, h2, h3 są wysokościami poprowadzonymi odpowiednio na te boki.

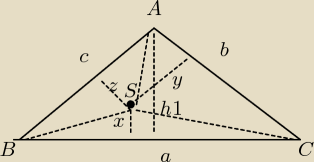AS: Pole całego trójkąta ABC jest sumą trójkątów BCS , ACS i ABS Stąd mamy

a*x		b*y		c*z		a*h1
	+		+		=
2		2		2		2

czyli a*x + b*y + c*z = a*h1 [1] Przyjmując podstawy dla całego trójkąta a,b i c mamy

a*h1		b*h2		c*h3
	=		=		z czego wyliczymy kolejno
2		2		2

	a*h1		a*h1
c =		. b =
	h3		h2

Podstawiając do [1] mamy

	a*h1*y		a*h1*z
a*x +		+		= a*h1 | : a*h1
	h2		h3

i otrzymuję wynik

x		y		z
	+		+		= 1
h1		h2		h3

Eta: P1= ax P₂= by P₃= cz P(ΔABC)= a*h₁= b*h₂= c*h₃ P₁+P₂+P₃= P( trójkąta ABC) ax +by +cz= ah₁= bh₂= ch₃ pierwszy składnik dzielimy przez ah₁ drugi przez bh₂ i trzeci przez ch₃

	ax		by		cz
		+		+		= 1
	ah1		bh2		ch3

	x		y		z
to:		+		+		= 1
	h1		h2		h3

c.n.u