Amelia: w prostokątnym układzie współrzędnych naszkicuj figurę F, gdzie F = {(x,y) : x, y ∈ R ^ 3 IxI + IyI ≤2}. oblicz pole figury F

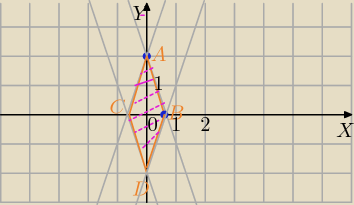
Lisek: 3 |x| + |y| ≤ 2 1. x,y≥0 3x+y≤2 y≤-3x+2 2. x,y<0 -3x-y≤2 y≥-3x-2 3. x≥0 y<0 3x-y≤2 y≥3x-2 4. x<0 y≥0 -3x+y≤2 y≤3x+2 Wierzchołki czworokąta mają współrzędne (0,2) (0,-2) (-2/3,0) (2/3,0). Jest to równoległobok więc długość jego przekątnych wynoszą: 4 i 4/3 P=1/2*4*4/3=8/3 j²

Kpsr: wszystko rozumiem do momentu kiedy napisales ze wierzchołki czworokąta mają współrzędne (0,2) (0,−2) (−2/3,0) (2/3,0). skad te wspolrzedne wziales? nie ogarniam

Vixen: rysujesz 4 proste y ( z tego co policzył kolega) zaznaczasz obszar pod lub nad y w zależności od równania, a wierzchołki powstają ze skrzyżowania tych 4 prostych

Milan: 3 |x| + |y| ≤ 2 Rozpatrujesz przypadki: 1) x≥0 i y≥0 wtedy masz nierówność: 3x+y≤2⇔y≤−3x+2 ( wykres tylko w i ćwiartce)

	2
miejsce zerowe x=
	3

punkty poniżej prostej y=−3x+2 2)x<0 i y≥0 ( II ćwiartka) −3x+y≤2 y≤3x+2 punkty poniżej prostej y=3x+2

	−2
miejsce zerowe x=
	3

3) x<0 i y<0 −3x−y≤2 −y≤3x+2 y≥−3x−2 punkty powyżej prostej y=−3x−2 III ćwiartka 4) x≥0 i y<0 3x−y≤2 −y≤−3x+2 y≥3x−2 punkty powyżej prostej y=−3x−2 IV ćwiartka

	1		4
PF=2*		*		*2
	2		3

Milan:

Vi: F(x)=1/2(x−3)⁺2