Zadanka do sprawdzenia Godzio: 1. Dla jakich wartości parametru a rozwiązaniem układu równań: x − ay = a ax − y = a jest para liczb z ktorych jedna jest sinusme a druga cosinusem tego samego kąta Czy o to chodzi ? : Zrobiłem to z wyznaczników, zał. W ≠ 0

	Wx
x =		= sinα
	W

	Wy
y =		= cosα
	W

sin²α + cos²α = 1 i z tego wyliczyć "a"

Godzio: Mając dane punkty A(−5,2) B(7,4) opisz za pomocą równania zbiór wszystkich punktów M takich, że

	π
|<AMB| =		. Co to za zbiór:
	2

jest to okrąg o środku odcinka AB i tylko napisać równanie tego okręgu: (x−1)² + (y−3)² = 37 D: R − {−5,7}

Godzio: Dla jakich wartości parametru m ∊ R odległość między wierzchołkami parabol określonych równaniami y = x² + 4x + 5 i y = −x² − 8x + m jest najmniejsza W(−2,1) W₁(−4,8 +m)

	−14
WW1 = ... = √m2 + 14m + 53 mw =		= −7
	2

I jeszcze ostatnie zadanko zaraz wrzucę

Godzio: Dla jakich wartości parametru m liczby x,y,z, spełniające równanie: 3x + 2y − 3z = 1 − 2m x + y + z = m + 4 2x − y + 2z = 2m + 2 tworzą w podanej kolejności ciąg geometryczny Moje rozw. 3x + 2y − 3z = 1 − 2m x + y + z = m + 4 2(x + z) = 2m + 2 + y bez zmian bez zmian x + z = m + 1 + 0,5y bez zmian m + 1 + 1,5y = m + 4 1,5y = 3 y = 2 3x + 4 − 3z = 1 − 2m 2x + 2z = 2m + 2 + 2 + −−−−−−−−−−−−−−−−−−−−−−−−−−− 5x − z + 4 = 5 4x − z = 1 4x − z = 1 => z = 4x − 1 x + y + z = m + 4 x + 2 + 4x − 1 = m + 4 5x = m + 3

	m+3
x =
	5

	4m + 12		4m + 7
z =		− 1 =
	5		5

y² = z * x

	4m + 7		m+3
4 =		*
	5		5

	4m2 + 12m + 7m + 21
4 =
	25

100 = 4m² + 19m + 21 0 = 4m² + 19m − 79 Δ = 1625 √Δ = 5√65

	−19 + 5√65
m1 =
	8

	−19 − 5√65
m2 =
	8

trochę nieciekawe wyniki ale nie mam coś na to pomysłu

Basia: w 1 i 2 wszystko gra; w 3 nie zgadza mi się rzędna W₁ wg mnie to 16+m reszta ok

Godzio: y = −x² − 8x + m

	8
p =		− 4
	−2a

f(−4) = − 16 + 24 + m = 8 + m

Godzio: więc chyba dobrze

Basia: ad.4 chyba mam prostsze rozwiązanie (jesli się nie pomyliłam) spróbuję napisać

Basia: Godzio eg mnie 8*4=32

Godzio: hehe no tak mnożenie mi się kłania

Basia: x, y=x*q, z=x*q² 3x+2xq−3xq²=1−2m x+xq+xq²=m+4 2x−xq+2xq²=2m+2 (1)+(3) 5x+xq−xq²=3 −−−−−−−−−−−−−−−−−−−−−−− x+xq+xq²=m+4 /*(−2) −2x−2xq−2xq²=−2m−8 2x−xq+2xq²=2m+2 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− −3xq=−6 q=⁶_3x=²_x 5x+x*²_x−x*⁴_x²=3 5x+2−⁴_x=3 5x²+2x−4=3x 5x²−x−4=0 Δ=1−4*5*(−4)=1+80=81 x₁=¹⁻⁹₁₀= −⁸₁₀= −⁴₅

	1+9
x2=		=1
	10

q₁= −2*⁵₄ = −⁵₂ q₂ = ²₁=2 x = −⁴₅ y = 2 z = −5 lub x=1 y=2 z=4

Basia: wyliczenie m chyba nie powinno już być problemem

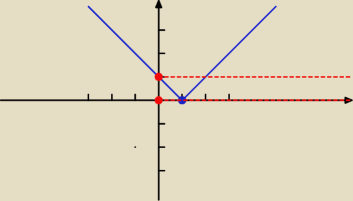
Godzio: I jeszcze ostatnie mi zostało: Dla jakich wartości parametru a równanie |x−1| = a² − 4a − 1 ma dwa pierwiastki dodatnie |x−1| = a² − 4a − 1 i domyślam się że a² − 4a − 1 to są proste jakieś tam, tylko jak wyznaczyć je żeby były w przedziale (0,1) ?

Godzio: Rzeczywiście, nie pomyślałem żeby od razu podstawić y = xq z = xq² Dzięki

Basia: no przecież wystarczy żeby a²−4a−1>0 i a²−4a−1<1

Godzio: ale jak tak obliczyłem to mi jakaś głupota wyszła, ale widocznie się pomyliłem

Godzio: a już wiem ... dałem a² − 4a − 1 > 0 i a² − 4a − 1 < 0 ...

Godzio: Dobra dzięki już wszystko rozumiem

Basia: a²−4a−1>0 Δ=16+4=20=4*5

	4−2√5
a1=		=2−√5
	2

a₂=2+√5 a∊(−∞,2−√5)∪(2+√5,+∞) a²−4a−2<0 Δ=16+8=24=4*6

	4−2√6
a1=		=2−√6
	2

a₂=2+√6 a∊(2−√6,2+√6) czyli ostatecznie a∊(2−√6,2−√5)∪(2+√5,2+√6)