pls mateos133: zad 1 Narysuj przekrój sześcianu o krawędzi 4 cm zawierające przekątne ścian równoległych sześcianu . Oblicz pole tego przekroju. zad 2 W ostrosłupie prawidłowym czworokątnym narysuj przekrój tak , aby zawierał sie w płaszczyźnie a) które zawiera dwa krawędzie boczne nie należącej do tej samej ściany b) dzielącej ten ostrosłup na dwie równe części , ale nie zawierającej przekątnej podstawy c) równoległej do jednej ze ścian bocznych ostrosłupa

Basia: za chwilkę, no za jakieś 15 minut

mateos133: ok

Basia: jeżeli weźmiesz BC musisz wziąć też AH, bo proste BC i DE są skośne i nie da się przez nie przeprowadzić płaszczyzny masz więc prostokąt o bokach |AB|=|GH|=a=4 i |BC|=|AH|=d gdzie d jest przekątną kwadratu o boku a=4 stąd d=a√2=4√2 P_ABGH=a*d=4*4√2=16√2

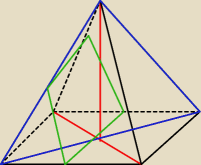
Basia: niebieski trójkąt to przekrój do (a) zielony trapez równoramienny to (c) (b) na drugim rysunku

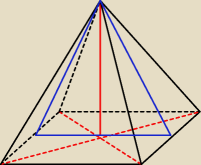
Basia: jeżeli mają powstać ostrosłupy przystające i płaszczyzna nie może zawierać przekątnej podstawy to musi zawierać odcinek łączący środki boków podstawy (przeciwległych) i wierzchołek ostrosłupa

mateos133: dzikęki