Oblicz długości boków trójkąta. Race, Bruce & Coroner: W trójkąt równoramienny ABC, w którym |AC| = |BC|, |∡C| = 120*, wpisano okrąg, którego promień ma długość 3cm. Oblicz długości boków trójkąta.

Race, Bruce & Coroner: Mogę liczyć na pomoc?

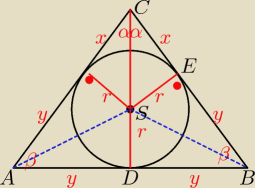
Basia: 2α=120 ⇒ α=60 ⇒ β=30 z tr.CDA

	y
sinα=
	x+y

	y
sin60=
	x+y

√3		y
	=
2		x+y

√3(x+y)=2y √3x+√3y=2y √3x=y(2−√3) z tr.CES

	x
ctgα=
	r

x=r*ctgα

	√3
x=3*ctg60 = 3*		=√3
	3

y(2−√3)=√3*√3 = 3

	3		3(2+√3)
y=		=		= 3(2+√3)=6+3√3
	2−√3		4−3

|AB| = 2y |AC|=|BC|=x+y dokończ obliczenia