matematykaszkolna.pl
długość boków trójkąta v: W trójkącie ABC długości boków AB i AC są odpowiednio równe 4 i 6, a długość środkowej AA' jest równa √10. Oblicz długość boku BC.
20 maj 17:55
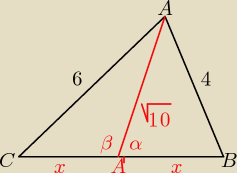
Basia: rysunekβ=180−α tw.cosinusów (tr.A'AB) x2=(√10)2+42−2*√10*4*cosα x2=10+16−8√10*cosα tw.cosinusów (tr.A'AC) x2=(√10)2+62−2*√10*6*cosβ x2=10+36−12√10*cos(180−α) x2=10+36−12√10*(−cosα) x2=10+36+12√10*cosα x2=46+12√10*cosα x2=26−8p{10)*cosα /*(−1) x2= 46+12√10*cosα −x2=−26+8√10*cosα −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 0=20+20√10cosα 20√10*cosα=−20
 20 1 
cosα= −
= −
 20√10 √10 
 1 
x2=26−8√10*(−
)
 √10 
x2=26+8=34 x=√34 |BC|=2x=2√34
20 maj 18:09
meduza: Basia Mnie wychodzi inny wynikemotka z tw. cosinusów: 42= x2+(√10)2−2*x*√10*cosα i 62= x2+√10)2−2*x*√10*cos(180o−α) , cos (180o−α)= − cosα x2+10 −2x√10*cosα= 16 x2+10 +2x√10*cosα= 36 + −−−−−−−−−−−−−−−−−−−− 2x2+20 = 52 => 2x2= 32 => x2= 16 => x= 4, bo x >0 to: IBCI= 2x= 8 jest wzór na środkową trójkąta d= 12 √2a2+2b2−c2 sprawdzam : d= 12√2*16 +2*36 − 82= 12√72+32−64= 12√40= 12*2√10 d= √10 czyli okemotka odp: IBCI= 8 −−−− jest poprawną odpowiedzią
20 maj 18:32
v: dzięki wielkie
20 maj 19:25
meduza: emotka
20 maj 19:26