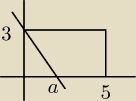
 Przyjrzyj się rysunkowi wyżej, zacieniowany obszar to ta część narysowanego prostokąta, która
leży poniżej prostej przechodzącej przez punty (0,3) i (a,0). Zapisz wzór funkcji, która
liczbie a przyporządkowuje pole tego obszaru.
Dla a w przedziale (0;5> umiem, ale z wyższymi liczbami mam problem
Przyjrzyj się rysunkowi wyżej, zacieniowany obszar to ta część narysowanego prostokąta, która
leży poniżej prostej przechodzącej przez punty (0,3) i (a,0). Zapisz wzór funkcji, która
liczbie a przyporządkowuje pole tego obszaru.
Dla a w przedziale (0;5> umiem, ale z wyższymi liczbami mam problem
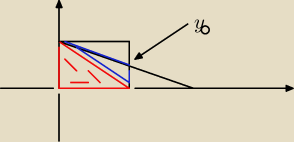 dla a>5 ta prosta przecina pionowy odcinek w punkcie o wspolrzednej y0 (ktora to wspolrzedna
trzeba sobie wyliczyc), wiec
f(a) = (15/2) + (1/2)*5*y0
15/2 to pole trójkąta prostokątnego − dolnej połowki prostokata − na rysunku czerwona, a
(1/2)*5*y0 to pole pozostalej zakreskowanej czesci − niebieskiej (jest to trojkat o podstawie
dlugosci y0 i wysokosci 5)
dla a>5 ta prosta przecina pionowy odcinek w punkcie o wspolrzednej y0 (ktora to wspolrzedna
trzeba sobie wyliczyc), wiec
f(a) = (15/2) + (1/2)*5*y0
15/2 to pole trójkąta prostokątnego − dolnej połowki prostokata − na rysunku czerwona, a
(1/2)*5*y0 to pole pozostalej zakreskowanej czesci − niebieskiej (jest to trojkat o podstawie
dlugosci y0 i wysokosci 5)

| 3−0 | ||
y−0 = | (x−a) | |
| 0−a |
| 3 | ||
y= − | (x−a) | |
| a |