. lolka: w okrąg o promieniu 7 wpisano czworokąt ABCD. Oblicz obwód L i pole P czworokąta , wiedząc , że : długość AB = długości BC ∡ADC = 120 stopni i stosunek P trójkąta ABD do pola trójkąta BCD jest równy 2:1

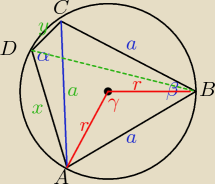
Basia: α=120 ⇒ β=60 ⇒ △ABC jest równoboczny ⇒ γ=120 stąd: a²=r²+r²−2r*r*cos120 = 2r²+2r²*¹₂ = 3r² a²=3*7² a=7√3 α+β=180 ⇒ |∡A|+|∡C|=180 P_ABD=¹₂a*x*sinδ P_BCD=¹₂*a*y*sin(180−δ)=¹₂*a*y*sinδ ^x_y=²₁ x=2y z tr.ADC a²=x²+y²−2xy*cos120 49*3 = (2y)²+y²−2*2y*y*(−¹₂) 5y²+2y²=49*3 7y²=49*3 y²=7³=21 y=√21 a=7√3 x=2√21 y=√21 resztę już sobie policz i sprawdź czy się gdzieś nie pomyliłam w rachunkach