geometria terminex: Zad. Podstawą graniastosłupa prostego jest trójkąt prostokątny o kącie ostrym równym 45 stopni. Jego przeciwprostokątna ma 8√2 cm. Przekątna ściany bocznej z krawędzią boczną tworzy kąt 60 stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa. Rozpatrz dwa przypadki

ANA: nie wiesz jak narysować czy w czym problem?

terminex: w rysunku trochę i coś mi zły wynik wychodzi

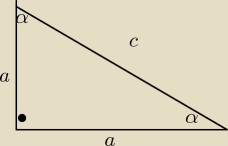
robinka: α=45 c=8√2 a=8 H= wysokość graniastosłupa Pierwszy przypadek tg60=H/a √3=H/8 8√3=H Pc=2Pp+Pb

	8*8
Pp=
	2

Pb=2*8*8√3+8√2*8√3 przypadek drugi tg60=H/c √3=H/8√2 8√6=H idalej liczmy analogicznie jak w przypadku pierwszym tak to liczyłeś ?

terminex: a bo to trygonometrią trzeba

robinka: tak

robinka: ja ci narysowałam podstawe

robinka: narysuje ci zaraz cały graniastosłup

terminex:

	64
w odpowiedzi jest		(3+2*√3+√6) − 1 przypadek
	3

64
	(3+2√6+2√3) − 2 przypadek
3

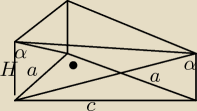
robinka: α=60 zauważyłam błąd w liczeniach założyłam zły kąt powinno być tg60=c/H oraz tg60=a/H

robinka: α=45 c=8√2 a=8 H= wysokość graniastosłupa Pierwszy przypadek tg60=H/a √3=H/8

8√3
	=H
3

Pc=2Pp+Pb Pp=32

	8√3		8P{3}
Pb=2*8*		+8√2*
	3		3

	√3		√6
Pc=64+128*		+64
	3		3

to jest taki sam wynik jak w odpowiedziach do pierwszego przypadku

terminex: aha dzięki