Oblicz pole trapezu D: W trapezie równoramiennym krótsza podstawa ma 9 cm, przekątna 17 a ramię 10 cm. Oblicz pole tego trapezu.

Anna: Pomagam

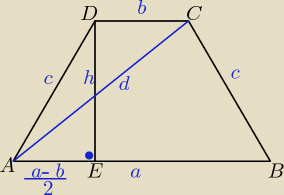
Anna: Dane: b = 9 cm, d = 17 cm, c = 10 cm P = ? Obliczam pole ΔACD o 3 danych bokach za pomocą wzoru Herona:

	b+d+c		9+17+10		36
P = √p(p−b)(p−d)(p−c), p =		=		=		= 18 cm
	2		2		2

P = √18(18−9)(18−17)(18−10) = √18*9*1*8 =36 [cm²]

	1
To samo pole: P =
	2*b*h

	1		2
Czyli:		*9*h = 36 ⇒ h = 36*		= 9 cm
	2		9

	a−b
Z ΔAED : (		)2 + h2 = c2
	2

	a−9
(		)2 + 82 = 92
	2

	(a−9)2
		+64 = 81
	4

	(a−9)2
		= 17 /*4
	4

(a−9)² = 68 ⇒ a−9 = √68 ⇒ a−9 = 2√17 ⇒ a = 2√17+9 Obliczamy pole trapezu:

	1		1
P =		(a+b)*h =		(2√17 + 9 + 9)*8 = (2√17 + 18)*4 =
	2		2

= 8(√17 + 9) cm²

Anna: Przepraszam, podstawiłam złą wartość za bok c do wzoru Pitagorasa. Już poprawiam.

D: ok, wielkie dzięki

D: już wiem jak to zrobić

D: dzięki za pomoc, nie musisz juz poprawiać

Anna:

	a−9
(		)2 + 82 = 102
	2

	(a−9)2
		+ 64 = 100
	4

	(a−9)2
		= 36
	4

(a−9)² = 144 ⇒ a−9 = 12 ⇒ a = 21cm

	1
P =		(21 + 9 ) * 8 = 4 * 30 = 120 cm2
	2

D: dzięki jeszcze raz^^

Anna:

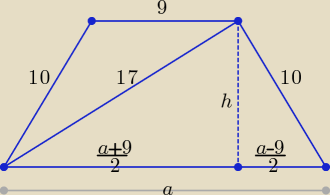Bogdan: Proponuję takie rozwiązanie:

	a + 9
(		)2 + h2 = 289
	2

	a − 9
(		)2 + h2 = 100 odejmujemy stronami
	2

− −−−−−−−−−−−−−−−−−−−−−−−−−

	a + 9 + a − 9		a + 9 − a + 9
		*		= 189 ⇒ a * 9 = 189 ⇒ a = 21
	2		2

	21 − 9
(		)2 + h2 = 100 ⇒ h = √100 − 36 = 8
	2

	21 + 9
Pole P =		* 8 = 120
	2