Geometria analityczna Boruc: ZAD 1. W trójkącie ABC mamy: |AC|=6 cm, |∡ CAB|=45^o, |∡ ACB|=15^o. Oblicz długości pozostałych boków trójkąta i długość promienia okręgu opisanego na tym trójkącie. ZAD 2. W trójkącie równoramiennym kąt przy wierzchołku ma miarę 120^o. Wyznacz stosunek długości promienia trójkąta opisanego na tym trójkącie do długości promienia okręgu wpisanego w ten trójkąt. ZAD 3. Oblicz miary kątów trójkąta, w którym wysokość i środkowa poprowadzone z jednego wierzchołka dzielą kąt przy tym wierzchołku na trzy równe części. ZAD 4. Oblicz długości przekątnych równoległoboku, jeśli jego boki mają długości a=2√3, b=3√2, a kąt ostry ma miarę 45^o ZAD 5. Oblicz cosinus kąta ostrego pomiędzy środkowymi trójkąta prostokątnego równoramiennego, poprowadzonymi z wierzchołków kątów ostrych. ZAD 6. Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym. ZAD 7. W trójkącie ABC dane są: |BC|=4cm, |AC|=2cm, |∡ ACB|=120^o. Wyznacz długość odcinka dwusiecznej kąta ACB, zawartego w tym trójkącie. Jeśli to nie problem prosiłbym o ew. rysunki do zadań (chodzi mi głównie o oznaczenia wierzchołków i innych punktów, co znacznie ułatwi zrozumienie podanego przez kogoś z Was rozwiązania). Z góry wielkie dzięki za pomoc.

Boruc: Help, please

Boruc: F5

Mc Ralph: Ref

Boruc: Pomoże ktoś?

Boruc: f5

Boruc: REF

Boruc: Może jednak ktoś się skusi?

Basia: Napisz każde zadanie w oddzielnym poście. Wtedy na pewno ktoś się skusi. Przy takim tasiemcu nie widzę w ogóle treści pierwszego o nie mam ochoty aż tak się męczyć. Inni pewnie też.

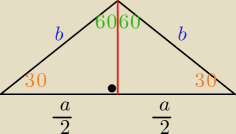
Eta: ze wzoru sinusów: R −− dł. promienia opisanego na trójkącie ABC

	b		b
2R=		=
	sin30o		12

to R= b r −− dł. promienia wpisanego w trójkąt ABC

	P
r=		, gdzie P −− pole p −−− połowa obwodu
	p

	√3
sin120o= sin(180o−60o)= sin60o=
	2

	b2		√3		b2√3
P= 12b*b*sin120o =		*		=
	2		2		4

	a2		√3
		= sin60o=
	b		2

	a		√3
to:		=		b
	2		2

a= b√3

	b+b+b√3		b(2+√3
p=		=
	2		2

	b2√3		2		b√3
r=		*		=
	4		b(2+√3)		2(2+√3)

	R		2(2+√3		2(2+√3)*√3
to:		= b*		=
	r		b√3		3

	R		2(2√3+3)
		=
	r		3

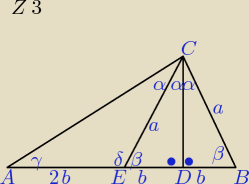
Basia: β=90−α δ=180−β=180−(90−α)=90+α α+δ+γ=180 α+90+α+γ=180 γ=90−2α z tr.BDC sinα=^b_a z tr.AEC

sinα		sinγ
	=
2b		a

ba		sin(90−2α)
	=
2b		a

b		cos2α
	=
2ab		a

1		cos2α
	=		/*a
2a		a

1
	=cos2α
2

2α=60 α=30, β=60, γ=30

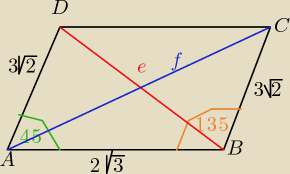
meduza: IBDI= e IACI= f α= 45^o β= 180^o−45^o= 135^o ze wzoru cosinusów:

	√2
e2= (3√2)2+ (2√3)2 −2*3√2*2√3*cos45o = 18+12 −12√3*√2*
	2

e²= 30 −12√3

	√2
podobnie f2 , cos135o= cos( 180o−45o)= −cos45o= −
	2

f²= 30 + 12√3 e= √30−12√3 f= √30+12√3

Basia: Liczę 7

meduza: Liczę 1/

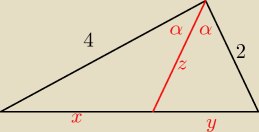
Basia: α=60 ^x_y=⁴₂=2 x=2y z.tw.cosinusów (x+y)²=4²+2²−2*4*2*cos120 (2y+y)²=16+4−16*(−¹₂) 9y²=20+8 9y²=28 y²=²⁸₉=^4*7₉

	2√7
y=
	3

ponownie z tw.cosinusów y²=z²+2²−2*z*2*cos60 ²⁸₉=z²+4−4z*¹₂ z²−2z+4−²⁸₉=0 z²−2z+³⁶⁻²⁸₉=0 z²−2z+⁸₉=0 Δ itd. pamiętaj, że 0 < z < 4

Basia: Liczę 6

meduza: 1/ miara trzeciego kąta: 180^o−(45^o+15^o)= 120^o ze wzoru sinusów:

	6
2R=
	sin120o

	√3
sin120o= sin(180o−60o) = sin60o=
	2

	2
2R= 6*		= 4√3
	√3

R=2√3

	a
podobnie:		= 2R= 4√3
	sin45o

	√2
a= 4√3*		= 2√6
	2

sin15^o= sin( 60^o−45^o)= sin45^o*cos30^o − sin30^o*cos45^o=

	√2		√3		1		√2		√2
=		*		−		*		=		( √3−1)
	2		2		2		2		4

	b
		= 2R
	sin15o

	√2
b= 2R*sin15o= 4√3*		*(√3−1)
	4

b= √2( 3−√3)

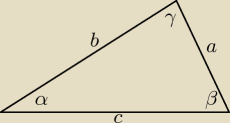
Basia: a, b=a*q, c=a*q² α, β=α+δ, γ=α+2δ α+β+γ=180 α+α+δ+α+2δ=180 3α+3δ=180 / :3 α+δ=60 β=60 z tw.cosinusów b²=a²+c²−2ac*cosβ (a*q)²=a²+(a*q²)²−2a*a*q²*¹₂ a²q²=a²+a²q⁴−a²q² / :a² q²=1+q⁴−q² q⁴−2q²+1=0 Δ=(−2)²−4*1*1=0 q²=²₂=1 q=1 (nie może ≠−1 bo wtedy długość boku b byłaby ujemna) stąd b=a*1=a c=a*1²=a czyli trójkąt jest równoboczny

Boruc: Dzięki wielkie