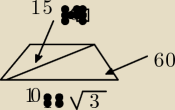
oblicz boki trapeza równoramennego o kacie 60 stopni i dłuzszej podsatwie 10 V3 a przekatnej 15
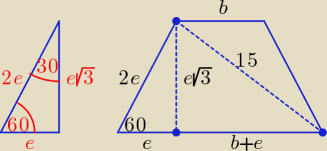Korzystamy z własności trójkąta o miarach kątów wewnętrznych: 30o, 60o. 90o.
Dłuższa podstawa: b + 2e = 10√3 ⇒ b = 10√3 − 2e
b + e = 10√3 − 2e + e = 10√3 − e
Na podstawie twierdzenia Pitagorasa: (b + e)2 + (e√3)2 = 152
(10√3 − e)2 + (e√3)2 = 225 ⇒ 300 − 20√3 + e2 + 3e2 = 225
4e2 − 20√3e + 75 = 0 ⇒ (2e − 5√3)2 = 0 ⇒ 2e = 5√3
b = 10√3 − 5√3 = 5√3
Odp.: Krótsza podstawa i ramiona trapezu mają długość 5√3.