Wzory na symetralne, dwusieczne i wysokości trójkąta Gustlik: Mam pytanko: szukam następujących wzorów: 1) na współrzędne punktu przecięcia symetralnych boków trójkata, 2) na współrzędne punktu przecięcia wysokości trójkata, 3) na współrzędne punktu przecięcia dwusiecznych trójkata. Wiem, jak to policzyć w zadaniu "na piechotę", ale jeżeli ktoś zna wzory lub link do odpowiedniej strony, bardzo proszę o pomoc, bo nie mogę ich znaleźć, a w tablicach ma tylko wzór na środek cieżkości trójkąta, czyli na punkt przecięcia środkowych.

Gabrysiaczek: Może to pomoże : http://matematyka.pl/post401052.htm#p401052

AS: Wzory takie można wyprowadzić,ale w praktyce mało przydatne z uwagi na ich złożoność. Prędzej wyliczy się rozwiązując układ równań,niż stosując wzór.

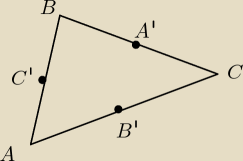
Lucyna: A = (x₁,y₁), B = (x₂,y₂), C = (x₃,y₃)potrzebne informacje, które łatwo wyliczyć: wektory CA = [CA_x,CA_y] = [x₁−x₃,y₁−y₃] i BA = [BA_x,BA_y] gdzie CA_x to pierwsza 'współrzędna' wektora CA reszta analogicznie. B' = (B'_x,B'_y) i C' = (C'_x, C'_y) to już wszystkie oznaczenia, współrzędne punktu przecięcia symetralnych boków trójkąta to:

	BAx   C'y+C'x   BAy
x =
	BAx   CAx   − BAy   CAy

	CAx		CAx		CAx
y = −		x + B'y + B'x		=		(B'x−x) + B'y
	CAy		CAy		CAy

w sumie nie takie koszmarne jakby się wydawało, ale średnio ciekawe do wykucia 'wzorku' na pamięć

Lucyna: ponieważ sama to liczyłam cóż nie twierdzę, że jestem nieomylna, ale mam nadzieję, że nie zrobiłam nigdzie byka rachunkowego i wzór działa. A jest już późno i nie chce mi się sprawdzać...

Lucyna: dobra sprawdziłam i jest błąd, jutro nad tym pomyślę

Gustlik: Dzięki Lucyno. Gabrysiaczku, tę metodę wskazaną w linku ja znam doskonale, sam zresztą nią robię. Mi chodziło o wzór, bo czasami jest on prostszy, niż układy równań, jak np. wzór na środek ciężkości trójkąta, ale równiez dzięki. Pozdrawiam Was obie.