Dane:bok 10cm,kąt 40^0.Oblicz długość przekątnych,pole,obwód rombu. Gabrysiaczek:

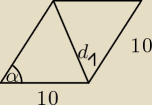
bzzz: z tw. cosinusów możemy obliczyć zarówno d₁ jak i d₂ d₁² = 10² + 10² − 2*10*10cos40 = 100(2 − 2cos40) d₂² = 10² + 10² − 2*10*10cos140 = 100(2 + 2cos40) d₁ = 10√2−2cos40 d₂ = 10√2+2cos40

	1
Pole rombu to		d1*d2 = 50√4−4cos240 = 100√1−cos240 = 100√sin240 = 100sin40
	2

Obwód to 4*10 = 40 cm.