Geometria analityczna
Godzio: Na okręgu:
(x+2)
2 + (y−3)
2 = 8
znajdź taki punkt A którego odległość od punktu P(2,7) jest najmniejsza.
Kompletnie nie wiem jak się za nie zabrać, może jakieś wskazówki
?
16 maj 23:43
Godzio: Myślałem o takim sposobie:
Wyznaczyć prostą yPS (S − środek okręgu}, znaleźć prostą prostopadłą styczną do kręgu, i
przyrównać ją do prostej yPS
16 maj 23:47
Bogdan:
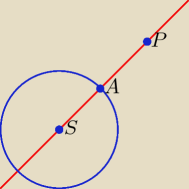
już wiesz ?
16 maj 23:54
bajka:
punkt A jest środkiem odcinka SP
16 maj 23:55
bajka:
16 maj 23:57
Bogdan:
Dzień dobry
Eto , lubisz bajki?, ja też
16 maj 23:57
Godzio:
Wszystko jasne, robiłem tak na początku tylko z tego co teraz widzę źle wyliczyłem prostą
Dzięki
16 maj 23:57
Godzio:
A czy z całą pewnością można określić, że A jest środkiem tego odcinka ?
16 maj 23:58
bajka:
Nawet bardzo
Witam
16 maj 23:59
bajka:
Ejjj
Godzio ........ masz jakieś wątpliwości
17 maj 00:00
Godzio: No już obliczyłem to nie
, ale gdyby punkt P był dalej odległy to A już nie byłby środkiem
17 maj 00:02
bajka:
wyznacz:
| | xS+xP | | yS+yP | |
xA= |
| =...... i yA= |
| =...... |
| | 2 | | 2 | |
17 maj 00:02
Godzio:
No tak tak, ale gdyby załóżmy P = (2,15) to już tak by nie było, także stąd moje wątpliwości
17 maj 00:04
Bogdan:
|PA| = |PS| − r, r = √8
17 maj 00:08