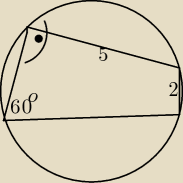
 Znajdź promień okręgu opisanego na czworokącie ABCD
Znajdź promień okręgu opisanego na czworokącie ABCD
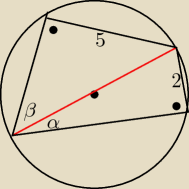 sinα=22r=1r
sinβ=52r
sinα=22r=1r
sinβ=52r
| 1 | r2−1 | |||
cos2α=1− | = | |||
| r2 | r2 |
| 25 | 4r2−25 | |||
cos2β=1− | = | |||
| 4r2 | 4r2 |
| √r2−1 | √4r2−25 | 1 | 5 | |||||
cos(α+β)=cosα*cosβ−sinα*sinβ= | * | − | * | = | ||||
| r | 2r | r | 2r |
| √r2−1*√4r2−25−1 | |
| 2r2 |
| √r2−1*√4r2−25−5 | 1 | ||
= | |||
| 2r2 | 2 |
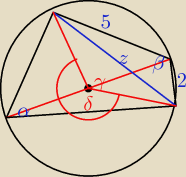 inny sposób:
α=60 ⇒ β=120
z2=22+52−2*2*5*cos120 = 4+25−20*(−12)=29+10=39
δ=2β=240 ⇒ γ=120
z2 = r2+r2−2*r*r*cos120=2r2−2r2*(−12) = 2r2+r2=3r2
3r2=39
r2=13
r=√13
inny sposób:
α=60 ⇒ β=120
z2=22+52−2*2*5*cos120 = 4+25−20*(−12)=29+10=39
δ=2β=240 ⇒ γ=120
z2 = r2+r2−2*r*r*cos120=2r2−2r2*(−12) = 2r2+r2=3r2
3r2=39
r2=13
r=√13