matma arek: oblicz pole trojkata w ktorym ,dwie srodkowe maja dlugosc 12 i 21 cm i przecinaja sie pod katem 45st

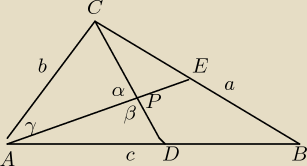
AS: P punkt przecięcia środkowych. Środkowe przecinają się w jednym punkcie i jedna z nich dzieli drugą w stosunku 2:1 licząc od wierzchołka. Przyjmuję: AE = 21 , CD = 12 , α = 45^o Z podanego twierdzenia mamy

	2
CP =		*CD = 8 , PD = 4
	3

	2
AP =		*AE = 14 , PE = 7
	3

Z ΔACD i tw.cosinusów b² = AP² + CP² − 2*AP*CP*cos(α) − mam już obliczone b Z ΔADP i tw. cosinusów mamy (β = 180^o − α) AD² = AP² + PD² − 2*AP*PD*cos(β) − mam już obliczone AD Ale D jest środkiem boku AB a więc AB = 2*AD − mam obliczony bok c Z ΔACD i tw.cosinusów mamy CD² = AD² + AC² − 2*AD*AC*cos(γ) stąd

	AD2 + AC2 − CD2
cos(γ) =		mam obliczony kąt γ
	2*AD*AC

Szukane pole

	1
P =		*AB*AC*sin(γ)
	2

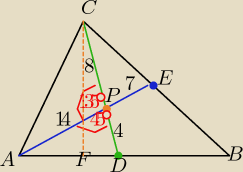bajka: Podaję inne rozwiązanie tego zadania : środkowe dzielą każdy trójkąt na dwa trójkaty o równych polach uzasadniam: PΔADC = PΔDBC ICFI= h −−− tych trójkątów i podstawy IADI= IDBI zatem PΔABC= 2*PΔADC PΔADC= PΔADP + PΔAPC

	√2
PΔADP= 1214*4*sin45o= 56*		= 28√2
	2

	√2
PΔAPC=12*14*8*sin135o=112*sin( 180o−45o)=112*sin45o=112*		=56√2
	2

to: PΔADC= 28√2+56√2= 84√2 więc PΔABC= 2*84√2= 168√2 [cm²] Pozdrawiam AS