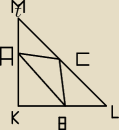
 W rownoramienny trojkat prostokatny KLM,w ktorym |KL|=|KM|=10, wpisano trojkat ABC tak,ze
AB||LM, punkt C jest srodkiem boku LM, a wierzchołki A i B naleza odpowiednio do ramion KM i
KL. zbadaj, w jaki sposob nalezy wybrac punkt A i B, aby pole trojkata ABC bylo najwieksze.
W rownoramienny trojkat prostokatny KLM,w ktorym |KL|=|KM|=10, wpisano trojkat ABC tak,ze
AB||LM, punkt C jest srodkiem boku LM, a wierzchołki A i B naleza odpowiednio do ramion KM i
KL. zbadaj, w jaki sposob nalezy wybrac punkt A i B, aby pole trojkata ABC bylo najwieksze.
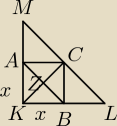 Skoro ramiona mają po 10cm to przeciwprostokątna ma 10√2
Skoro wierzchołek C leży dokładnie po środku przeciwprostokątnej to dzieli ją na dwa odcinki o
długości 5√2
Z faktu, że AB jest równoległa do ML wynika, że trójkąt AKB jest podobny do MKL zatem skoro
jest podobny to też jest równoramienny, czyli AK = x = KB i AB = x√2
Ponieważ interesuje nas pole max
Skoro ramiona mają po 10cm to przeciwprostokątna ma 10√2
Skoro wierzchołek C leży dokładnie po środku przeciwprostokątnej to dzieli ją na dwa odcinki o
długości 5√2
Z faktu, że AB jest równoległa do ML wynika, że trójkąt AKB jest podobny do MKL zatem skoro
jest podobny to też jest równoramienny, czyli AK = x = KB i AB = x√2
Ponieważ interesuje nas pole max
| 1 | ||
P = | ABh, gdzie h = CK − KZ ( CK = CL wynika to z podobieństwa trójkątów), więc | |
| 2 |
| x√2 | ||
h=5√2− | ||
| 2 |
| 1 | x√2 | |||
Zatem nasz wzór na pole to P= | x√2(5√2− | )
| ||
| 2 | 2 |