ZNAJDŹ EKSTREMUM FUNKCJI cz.2 olx: Chciałabym jeszcze prosić o pomoc w rozwiązaniu dwóch przykładów, gdyż w ogóle nie wiem jak sie za nie zabrac: 1) f(x)=x−√x

	1
doszłam jedynie do pochodnej −> f'(x)=1−		i nie wiem gdzie szukać ekstremum....
	2√x

2) f(x)=|x²−5x−5| no tutaj jedynie doszłam do tego:

	⎧	x2−5x−6 dla x2−5x−6 ≥ 0
|f(x)| =	⎩	−x2+5x+6 dla x2−5x−6 < 0

i całkiem nie wiem co i jak dalej...

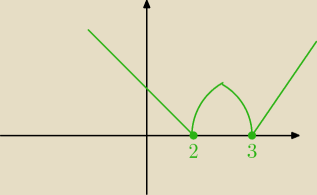
Amaz: to wykres funckji do zadania 2. Myślę, że nie trzeba tutaj pochodnych by odczytać extrema

Amaz: oczywiście to wykres paraboli, ale nie wiem jak to tutaj narysować

paziówna: ja bardzo chętnie Ci pomogę ekstremów(ewentualnie punktów przegięcia) szukasz poprzez przyrównanie pierwszej pochodnej do 0. w 1) zał. x≥0

	1
f'(x) = 1 −		zał. x≠0
	2√x

f'(x) = 0

	1
1 −		= 0
	2√x

2√x − 1
	= 0
2√x

2√x − 1 = 0

	1
√x =		/()2
	2

	1
x =
	4

	1
dla x =		funkcja f przyjmuje ekstremum. teraz badamy, czy minimum, czy maksimum:
	4

	1
x∊(0,		): f'(x)<0 ⇔ f maleje
	4

	1
x∊(		, +∞): f'(x)>0 ⇔ f rośnie
	4

	1
jeśli po lewej stronie ekstremum funkcja maleje, a po prawej rośnie, to x =		jest
	4

minimum funkcji f

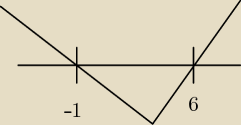
olx: co do 1 przykładu to funkcja podstawowa miala byc oczywiscie f(x) = f(x)=|x²−5x−6| , pomylilam sie przepisujac (zamiast 6 napisalam 5) ale tam dalej juz napisalam ok. NIe rozumiem niestety skad sie wzial te wykres liczas miejsca zerowe z delty wychodzi mi x− −1 i x=6... nadal nie za bardzo wiem jak sie za to zabrac. paziówna dziekuje tylko mam jeszcze pytanie jak to rozwiazanie narysowacna wykresie?

Amaz: nom masz racje źle policzyłem x₁ i x₂ czyli wyniki to −1 i 6, wykres możesz narysować tak samo, tylko po prostu zmień miejsca zerowe

olx: a czemu ten wykres odbija sie w tych miejscach zerowych?

Amaz: no bo masz wartość bezwzględną nałożoną na całą funckje, czyli funkcja nie może przyjmować, żadnych wartości ujemnych, czyli to co jest pod osią OX odbija się w górę.

olx: no kurcze racja, dziekuje

olx: to w takim razie funkcja nie ma ekstremów , bo nie zmienia nigdzie znaku?

Amaz: nie, nie to pochodna ma zmieniac znak, wtedy wiemy kiedy funckja maleje a kiedy rośnie, tutaj nie liczyliśmy pochodnej, tylko narysowaliśmy wykres. Te extrema odczytaj po prostu z wykresu Liczenie pochodnej w tym przykladzie wg mnie byłoby czymś niefajnym, bo trzeba by bylo rozpatrywać przypadki i łatwo jest się pomylić...

olx: a jak z tego wykresu zrobic wykres pochodnej?

Basia: nie robić; policzyć rachunkowa tak jak pokazała paziówna

olx: no tak... tylko rachunkowo nie wiem jak sie zabrac za rozwiązanie przykładu 2...

paziówna: 2) x² − 5x − 6 = (x+1)(x−6) {x² − 5x − 6 dla x∊(−∞, −1)∪(6,+∞) f(x)= {−x² + 5x + 6 dla x∊[−1,6] {2x − 5 dla x∊(−∞,−1)∪(6,+∞) f'(x)= {−2x + 5 dla x∊[−1,6] f'(x) = 0 ⇔ 2x−5=0 ∧ −2x+5=0

	5
x =
	2

x∊(−∞,−1)∪(6,+∞) brak rozw.

	5
gdyby na chwilkę założyć, że funkcja y=x2 − 5x − 6 jest na całą dziedzinę, to xw=
	2

	5
więc dla x∊(−∞,		) f maleje
	2

	5
x∊(		, +∞) f rośnie
	2

powracając do naszego zadania: x∊(−∞,−1) f maleje x∊(6,+∞) f rośnie patrzysz na f'(x) = −2x + 5 bo teraz patrzymy, co się dzieje w przedziale [−1,6]

	5
x∊[−1,		) f'>0 f rośnie
	2

	5
x∊(		,6] f'<0 f maleje
	2

	5
x=		maksimum lokalne
	2

olx: dziekuje !