geometria analityczna fruu: Dane są wierzchołki A(−1,4) i C(6,−1) trójkąta ABC. Oblicz pole tego trójkąta, jeśli jego środkowe przecinają się w punkcie S(1,−2).

Basia: Pomagam

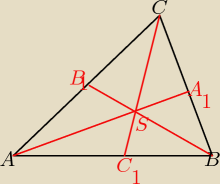
Basia: 1. oblicz współrzędne AC^→ 2. oblicz współrzędne AS^→ 3. oblicz współrzędne SB^→ 4. oblicz współrzędne AB^→=AS^→+SB^→ 5. P_ABC = ¹₂|AB^→|*|BC^→|*|sin∡(AC^→,AB^→)|

	a1*b2−a2*b1
sin∡(AB→,AC→) =
	|AB→|*|AC→|

stąd: P_ABC = ¹₂*|a₁*b₂−a₂*b₁| gdzie a₁,a₂ to współrzędne AC^→, b₁,b₂ to współrzędne AB^→

fruu: spoko, ale kurcze nie mam danych do punktu A (x,y) wiec ?

fruu: znaczy B Xd

Basia: a rzeczywiście no to tak: SC₁^→=¹₂SC^→ liczysz wsp.SC^→ i masz po pomnożeniu przez ¹₂ wsp.SC₁^→ stąd znajdziesz wsp.C₁ pr.AB = pr.AC₁ piszesz jej równanie SA₁^→=¹₂SA^→ liczysz wsp.SA^→ i masz po pomnożeniu przez ¹₂ wsp.SA₁^→ stąd znajdziesz wsp.A₁ pr.BC = pr.CA₁ piszesz jej równanie punkt B jest p−tem wspólnym pr.AB i pr.BC rozwiązujesz układ równań liczysz wsp. AB^→ i AC^→ i korzystasz z wzoru, który przedtem podałam

fruu: prosiłbym tylko o podanie, skąd się wzięło takie coś: SC₁^→=¹₂SC^→ jest na to jakieś twierdzenie?

fruu: oke, jest twierdzenie =)) dziękuje ślicznie za pomoc Basiu!

Gustlik: Dane są wierzchołki A(−1,4) i C(6,−1) trójkąta ABC. Oblicz pole tego trójkąta, jeśli jego środkowe przecinają się w punkcie S(1,−2). Wzór na wspólrzędne środka cieżkości, czyli punktu przecięcia środkowych:

	xA+xB+xC		yA+yB+yC
S=(		,		)
	3		3

A(−1,4) B(x, y) C(6,−1) S(1,−2) Liczę współrzędne B:

	−1+x+6		4+y−1
S=(		,		)=(1, −2)
	3		3

−1+x+6
	=1 /*3
3

−1+x+6=3 x=3+1−6 x=−2

4+y−1
	=−2 /*3
3

4+y−1=−6 y=−6−4+1 y=−9 B(−2, −9) Wierzchołki trójkąta: A(−1,4) B(−2, −9) C(6,−1) Liczę współrzędne wektorów AB^→ i AC^→ AB^→=B−A=[−2−(−1), −9−4]=[−1, −13] AC^→=C−A=[6−(−1), −1−4]=[7, −5] Liczę wyznacznik wektorów d(AB^→, AC^→) d(AB^→, AC^→) = |−1 −13| |7 −5 | −1*(−5)−(−13)*7=5+91=96

	1		1
P=		|d(AB→, AC→)|=		*96=48
	2		2