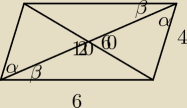
Oblicz pole równoległoboku. PhoenixIV: Równoległobok ma jeden bok 4 a drugi 6 oraz kąt między przekątnymi 60°. Oblicz pole tego równoległoboku.

Jasiek: https://matematykaszkolna.pl/strona/863.html

PhoenixIV: Tak to spróbuj za pomocą tego co napisałeś rozwiązać to zadanie....

Kejt: proponowałabym bycie trochę milszym.. bo tak to nikt w tej sprawie palcem nie kiwnie..

PhoenixIV: I tak nikt nie kiwnie w tej sprawie palcem bo nikt prawdopodobnie nie wie jak to zrobić...

paziówna: yy nikt nie wie, jak to zrobić? ciężko skorzystać ze wzoru "P = absinα" (α−kąt między bokami a, b)

Amaz: tutaj kąt jest pomiedzy przekątnymi

paziówna: no tak, teraz zadanie wskakuje na taki poziom, że nikt sobie z nim nie poradzi...

paziówna: {4² = x² + y² − 2xycos60^o {6² = x² + y² − 2xycos120^o (mała podpowiedź: cos120^o = cos(180^o − 60^o) = −cos60^o) mając x i y z tw. cosinusów wyliczysz α i β. koniec zadania.

PhoenixIV: Dzięki za rozwiązanie. Nie żeby coś ale nie umiałem dobrze ocenić tego zadanie bo jestem dopiero w 3 gimnazjum a nasz pan sam nam je zadał a potem nie chciał nam pokazać jak je zrobić

paziówna: 3 gimnazjum?! ej to Ty nie miałeś(aś?) twierdzenia cosinusów to wykminie jakiś inny sposób

Basia: funkcji trygonometrycznych też nie; będzie ciężko, a możliwe, że wcale się nie da; chyba dlatego pan nie chciał podać rozwiązania

paziówna: no, racja, trygonometrii też nie ma... no daj spokój, to po co w ogóle podają ten kąt

Basia: myślę, że nauczyciel "się rąbnął" i dał dzieciakom zadanie nie na ich poziom i tyle, bo naprawdę nie widzę sposobu rozwiązania tego bez trygonometrii;

Dudi: W sumie, no to trzeba pokombinować. Nam ciągle też dają w 3 gimn zadania z kątami i ja je z trygonometrii, lub innego sposobu rozwalam − dzięki temu czasami jestem "geniuszem" klasowym, a czasami "debilem" . Spróbować zawsze można z własności trójkątów o kątach 60, 30, 90 oraz 90, 45, 45.

Dudi: Albo zrób za pomocą trygonometrii, nauczyciel pomysli, ze sie rozwinąłeś intelektualnie.

PhoenixIV: Ja to zrobiłem tak:

	4(x*y)
Wyprowadziłem z tego układu x*y=10 i podstawiłem pod wzór P=		*sinφ (4 razy bo to są
	2

połowy tych przekątnych) czyli P=10√3

PhoenixIV: Acha co do tego że f−cje trygonometryczne to my właśnie je zaczynamy bo nauczyciel postanowił że zrobimy wcześniej to w liceum będzie łatwiej

PhoenixIV: I jeżeli chodzi o jakieś wzory to mogę używać wszystkiego bylebym potrafił to powtórzyć w klasie to zadanie jest po prostu jako dodatkowe.

PhoenixIV: Bo pan napisał 3 zadania na tablicy w tym to jako trudniejsze (na 6) po 5 minutach patrzy i oznajmia wszystkim ze i tak go nie zrobimy bo to nie nasz poziom

Bogdan: Dzień dobry. Myślę, że najprościej jest rozwiązać to zadanie stosując twierdzenie cosinusów.

	1		1		3
cos60o =		, cos120o = −		, sin60o =
	2		2		2

	1		3
Pole równoległoboku P =		*2x*2y*sin60o = 2xy*		= xy√3
	2		2

ΔABS: x² + y² − 2xycos120^o = 36 ΔBCS: x² + y² − 2xycos60^o = 16 x² + y² + xy = 36 x² + y² − xy = 16 odejmujemy równania stronami − −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 2xy = 20 ⇒ xy = 10 P = 10√3

PhoenixIV: Właśnie tak zrobiłem (w innej kolejności ale tak samo)