trójkąty Lusia: punkt styczności okręgu wpisanego w trójkąt prostokątny dzieli jedną z przyprostokątnych na odcinki o długościach 2 cm i 4 cm. Oblicz: obwód trójkąta, pole trójkąta i pole kola wpisanego i opisanego na tym trójkącie.

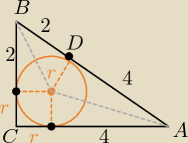
bajka: c= IABI= 6 a= ICAI= r+4 b= ICBI= r+2 z tw. Pitagorasa a²+b² = c² => ( r+4)² + ( r+2)²= 36 r²+8r+16 +r² +4r +4−36=0 2r²+12r−16=0 r² +6r−8=0 Δ= 68 √Δ= 2√17 i r >0

	−6+2√17
r=		= √17−3
	2

a= √17+1 b= √17−1 Ob= √17+1 +√17−1 +8= 2√17+6 = 2( √17+3) cm

	a*b
P=		= ..........dokończ
	2

R −− okręgu opisanego : R= ^c₂= 3 P(koła wpisanego) = πr² =.......... P(koła opisanego)= πR²=.......

Lusia: Dziękuję

Stella: Jedna z przyprostokątnych dzieli się na odcinki. U Ciebie zaznaczona jest przeciwprostokątna.