: Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem 30 stopni. Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa. Jak do tego sie zabrać ? Dodam że nie bardzo umiem trygonometrię krawędź sześciany będę juz umiec obliczyć, ale z tym ostrosłupem ciężko

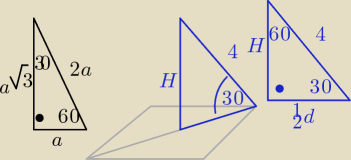
Godzio: d=a√2 jeśli nie umiesz zbytnio trygonometrii to możesz z zależności w danym trójkącie, z tego wynika,że: 2H = 4 H = 2

1
	d = 2√3
2

a√2 = 4√3 a = 2√6

	1		1		2
V =		*H* Pp =		* 2 * (2√6)2 =		* 6 * 4 = 16
	3		3		3

V = V_sześcianu 16 = a³ 2³√2 = a