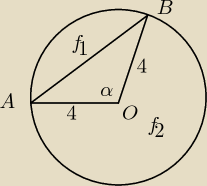
Dł. okręgu i pole koła Ewuś: W kole o środku O i promieniu 4 poprowadzono cięciwę AB. Oblicz pola figur na jakie cięciwa podzieliła koło jeśli pole trójkąta AOB jest równe 4√2

Godzio:

	1
PΔ =		* 42 * sinα = 4√2
	2

2sinα = √2

	√2
sinα =		=> α = 45o
	2

P_koła = πr² = 16π

	45
Pw =		* πr2 = 2 π
	360

P_f1 = P₂ − P_Δ = 2π − 4√2 P_f2 = P_koła − P_f1 = 16π − 2π + 4√2= 14π + 4√2

Jarass: Czy jest może drugie rozwiązanie bo sinα = ^√2 ₂ => α = 45^o lub 135^o ?