Oblicz pole równoległoboku (f-cje trygonometryczne)
PhoenixIV: Jako że nasz matematyk rozpoczął funkcje trygonometryczne w 3 gimnazjum to postanowił zacynić i
zadał nam zadanie na 6.
Zadanie: (podobno mamy jakoś wykorzystać twierdzenie sinusów) Równoległobok ma jeden bok 4 a
drugi 6 oraz kąt między przekątnymi 60°. Oblicz pole tego równoległoboku.
13 maj 14:03
Tomek.Noah: NIe wiesz jak to zrobic?
13 maj 14:29
PhoenixIV: No jakbym wiedział to bym się nie pytał? Prawdopodobnie jest to w miarę proste ale nie mogę
tego złapać

13 maj 14:39
PhoenixIV: Wiem na pewno że mam dane po jednym boku i jednym kącie naprzeciwko boku...
13 maj 14:41
Tomek.Noah:
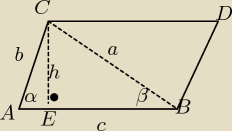
Dla ΔAEC:
| | 1 | | 1 | |
P= |
| c*h => P= |
| c*bsinα |
| | 2 | | 2 | |
Dla ΔABC:
z tw. sinusow wynika rownosc
| a | | b | |
| = |
| gdzie a=b*sinα |
| sinα | | sinβ | |
zatem
| | 1 | | 1 | |
P= |
| c*b*sinα= |
| c*a*sinβ |
| | 2 | | 2 | |
| | 1 | |
masz podane c i b i α zatem Pole ΔABC = |
| b*c*sinα wiem rowniez ze ΔABC=ΔBCD |
| | 2 | |
zatem Pole rownolegloboku bedzie rown 2P
ΔABC czyli P=cbsinα
b=4 c=6 α=60
| | √3 | |
P=4*6*sin60o=24* |
| =12√3 |
| | 2 | |
13 maj 14:50
Tomek.Noah: aj sry mysklalem ze kat miedzy bokami
13 maj 14:51
Tomek.Noah: ale to juz proste masz wzor tylko znajdz kat i juz

13 maj 14:51
PhoenixIV: No właśnie chodzi o to że nie potrafię znaleźć tego kąta... Tak jakbym go znalazł to byłoby
wszystko gites.
13 maj 15:29
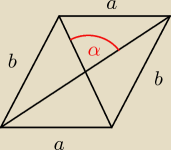
Kejt:
13 maj 15:32
PhoenixIV: Tak mniej więcej tyle danych mam z zadania

13 maj 15:35
PhoenixIV: A brak mi któregoś kąta równoległoboku albo chociaż jednego z trójkątów...
13 maj 15:36
Kejt: szukałeś kąta..?
13 maj 15:36
PhoenixIV: No a niby w jaki sposób? Bo jakoś nie znam żadnych lepszych niż α+β+60=180 i innych
podobnych...
13 maj 15:39
PhoenixIV: Ale chyba mam pomysł
13 maj 15:39
Kejt:
hmm..
P=a*b*sinα?
13 maj 15:40
PhoenixIV: No nie widać że z tego wzoru nic nie dostaniesz?
13 maj 15:49
Kejt:
α=60o
sinα=0,866
P=4*6*0,866=20,784
hmm.. może tak. nie wiem czy to dobrze, ale..
13 maj 15:55
ala: Rownoleglobok rozwarcie bokoe 45
12 maj 10:04
prosta:
| | ef√3 | |
e,f−przekątne równoległoboku P=0,5efsin60o ⇒ P= |
| |
| | 4 | |
x=0,5e i y=0,5f
z tw. cosinusów:
| | 1 | |
62=x2+y2−2xycos120o , cos1200=cos(180o−60o)=−cos60o=− |
| |
| | 2 | |
4
2=x
2+y
2−2xycos60
o
po odjęciu stronami otrzymujemy:
20=xy+xy
xy=10 ⇒ ef=(2x)(2y)=4xy=40
12 maj 14:07

 Dla ΔAEC:
Dla ΔAEC:


