GGGGD !!!!!!!!!!!!!!!!!!!!!!: ILE OS SYMETRII MA KOLO I JAK TO NARYSOWAC ?

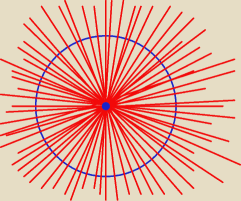
Filip: Koło ma nieskończenie wiele osi symetrii, każda średnica jest jednocześnie osią symetrii.

ewa:

ufo:

Marcin: ufo! Jak dla mnie, to ma więcej

qu: 54 jak dobrze policzyłem

ufo:

bezendu: Milion 500 sto 900 taka jest odp

hugo: lim₁→∞

PW: Śmichy śmichami, ale poważnie powinno to być tak: Teza: Każda prosta zawierająca środek okręgu jest jego osią symetrii. Dowód: Kto chętny?

qu: zaciekawiłeś mnie tym dowodem ja się nie czuje na siłach ale chętnie zobaczę jak to powinno wyglądać

Ajtek: Gdzieś to chyba, kiedyś robiłem / miałem zrobić. Chyba w szkole średniej... Witam PW, bezendu .

PW: Dowód jest banalny; dawno,dawno temu uczyłem dzieci w piątej klasie szkoły podstawowej (jeszcze nie było gimnazjów) i każdy musiał umieć. Rozważmy symetrię o osi k zawierającej środek S okręgu. Weźmy dowolny punkt P należący do okręgu, to znaczy taki że, |PS| = r. Z definicji symetrii wynika, że jeśli P∊k, to obrazem P jest ten sam punkt P. Weźmy więc P spoza k. Obrazem P w symetrii jest pewien punkt P'≠P, a obrazem S jest ten sam punkt S. Symetria osiowa jest izometrią (nie zmienia odległości punktów), a więc odległość między obrazami P i S jest taka sama jak między tymi punktami: |P'S| = |PS| |P'S| = r. Oznacza to, że dla dowolnego punktu P okręgu jego symetryczny obraz też należy do tego okręgu − innymi słowami obraz okręgu w symetrii o osi k zawierającej jego środek jest tym samym okręgiem.