Eta:
I x
2 −9I
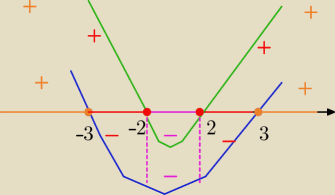
_________ miejsca zerowe x= −3 v x= 3
Ix
2−4I
_________ miejsca zerowe x= −2 v x= 2
" + " −−− po opuszczeniu modułu nie zmieniamy znaków
" − " −−−−− " " " " zmieniamy znaki
1/ dla x€ ( −∞, −3 > U < 3,∞) mamy:
x
2 −9 +x
2 −4=5
2x
2= 18 => x
2= 9 => x= 3 v x= −3 −−− są rozwiązaniami w tym przedziale
2/ dla x€ ( −3, −2> U <2 , 3)
−x
2 +9 +x
2 −4 =5
5=5 −−− równanie tożsamościowe w tym przedziale
rozwiązaniem jest cały przedział: x€ (−3, −2> U < 2, 3)
3/
dla x€ ( −2, 2)
−x
2 +9 −x
2 +4=5
−2x
2= −8 => x
2= 4 => x= −2 v x = 2 −−− nie są w tym przedziale
rozwiązaniem pierwotnego równania jest suma wszystkich rozwiązań:
odp:
x€ < −3, −2> U < 2, 3>
 I x2 −9I _________ miejsca zerowe x= −3 v x= 3
Ix2−4I _________ miejsca zerowe x= −2 v x= 2
" + " −−− po opuszczeniu modułu nie zmieniamy znaków
" − " −−−−− " " " " zmieniamy znaki
1/ dla x€ ( −∞, −3 > U < 3,∞) mamy:
x2 −9 +x2 −4=5
2x2= 18 => x2= 9 => x= 3 v x= −3 −−− są rozwiązaniami w tym przedziale
2/ dla x€ ( −3, −2> U <2 , 3)
−x2 +9 +x2 −4 =5
5=5 −−− równanie tożsamościowe w tym przedziale
rozwiązaniem jest cały przedział: x€ (−3, −2> U < 2, 3)
3/
dla x€ ( −2, 2)
−x2 +9 −x2 +4=5
−2x2= −8 => x2= 4 => x= −2 v x = 2 −−− nie są w tym przedziale
rozwiązaniem pierwotnego równania jest suma wszystkich rozwiązań:
odp: x€ < −3, −2> U < 2, 3>
I x2 −9I _________ miejsca zerowe x= −3 v x= 3
Ix2−4I _________ miejsca zerowe x= −2 v x= 2
" + " −−− po opuszczeniu modułu nie zmieniamy znaków
" − " −−−−− " " " " zmieniamy znaki
1/ dla x€ ( −∞, −3 > U < 3,∞) mamy:
x2 −9 +x2 −4=5
2x2= 18 => x2= 9 => x= 3 v x= −3 −−− są rozwiązaniami w tym przedziale
2/ dla x€ ( −3, −2> U <2 , 3)
−x2 +9 +x2 −4 =5
5=5 −−− równanie tożsamościowe w tym przedziale
rozwiązaniem jest cały przedział: x€ (−3, −2> U < 2, 3)
3/
dla x€ ( −2, 2)
−x2 +9 −x2 +4=5
−2x2= −8 => x2= 4 => x= −2 v x = 2 −−− nie są w tym przedziale
rozwiązaniem pierwotnego równania jest suma wszystkich rozwiązań:
odp: x€ < −3, −2> U < 2, 3>