prosze niech ktos mi to wytłumaczy z nierówności
sebas: a) I x−3 I>5
b) I x+2 I<4
jak to sie rozwiazuje bo nie rozumie

9 maj 15:49
Kejt:
a) |x−3}>5
x−3>5 v x−3<−5
drugie analogicznie.
9 maj 16:16
sebas:

kejt a jak narysowac sie ten wykres
wiesz cos takiego i jak wyznaczyc X∊

9 maj 16:23
Kejt:
x−3>5
x>8
x∊(8;∞) jeśli się z nawiasami nie pomyliłam, to to będzie coś takiego..
9 maj 16:30
sebas:

dokładnie to miałem na lekcji rozwiązane tak do tego a)
X∊ (−8;−2) ∪ (8 +8)
dlaczego to tak ma byc moze ktos wyjasnic

9 maj 16:40
Godzio:

b)
| x + 2 | < 4 => znajdujemy miejsce zerowe x
o = −2 bo | x − x
o | < a => |x − (−2)| < 4
teraz idziemy w lewo i w prawo o a jednostek, w tym wypadku a = 4 i szukamy punktów odległych
mniej niż o 4 jednostki od x
o
9 maj 16:45
Kejt: rozwiązałeś tamte równania?
9 maj 16:45
sebas: nie to bylo ostatnio na lekcji ale ja nic z tego nie rozumie
to nie bylo rozwiazywane ani nic tylko tyle
9 maj 16:47
Godzio: albo rozwiązujemy normalnie:
|x + 2| < 4
x + 2 < 4 ∧ x + 2 > − 4
x < 2 ∧ x > − 6
x∊(−6,2)
Zapamiętaj jeśli mamy nierówność | x − x
o | > a => to rozpisując ją tak jak wyżej dajemy "lub"
= "v" co oznacza sume zbiorów
ja to tak zapamiętuje ze znaczek skręca o 90
o w prawo ">"−> "v"
Jeśli mamy | x − x
o | < a => dajemy pomiędzy nierówności znaczek "i" = "∧" − co oznacza część
wspólną i tak samo o 90
o 
=> "<" −> "∧"
9 maj 16:49
Kejt: ups..nierówności*
9 maj 16:50
Godzio:
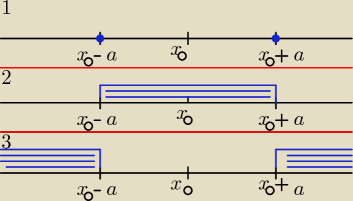
Teraz tak ogólnie zapisane:
1.
|x − x
o| = a
2.
|x − x
o| < a
3.
|x − x
o| > a
Zapamiętaj
|x − x
o| < 0 − sprzeczność bo |x| ≥ 0
|x − x
o| > −1 −> x∊R bo |x| ≥ 0
9 maj 16:55
9 maj 16:56
Kejt:
x−3>5 v x−3<−5
x>8 v x<−2
więc:
x∊(8;∞) v x∊(−∞;−2)
zasada jest taka, że po lewej stronie musi być zawsze liczba mniejsza.. 8<∞
btw. ∞ to nieskończoność.
9 maj 16:56
Kejt: Godzio.. że Tobie się chce to rysować.. ja jestem zbyt leniwa..
9 maj 16:58
Godzio: nie ma nic ciekawego do roboty to co mi tam

9 maj 16:59
ala: Z definicji wartości bezwzględnej wynika, że jezeli określamy wartość bezwzględną liczby≥0 to
jest ona równa tej liczbie, a jeżeli określamy wartość bezwzględną liczby<0 to jest ona równa
liczbiedo niej przeciwnej, czyli:
1) jeżeli x−3<0 to −x+3>5 stąd x<3 i x<−2 czyli x<−2
2) jeżeli x−3≥0 to x−3>5 sąd x>8
Tak samo rozwiązujemy drugi przykład
9 maj 22:16

 kejt a jak narysowac sie ten wykres
wiesz cos takiego i jak wyznaczyc X∊
kejt a jak narysowac sie ten wykres
wiesz cos takiego i jak wyznaczyc X∊
 dokładnie to miałem na lekcji rozwiązane tak do tego a)
X∊ (−8;−2) ∪ (8 +8)
dlaczego to tak ma byc moze ktos wyjasnic
dokładnie to miałem na lekcji rozwiązane tak do tego a)
X∊ (−8;−2) ∪ (8 +8)
dlaczego to tak ma byc moze ktos wyjasnic
 b)
| x + 2 | < 4 => znajdujemy miejsce zerowe xo = −2 bo | x − xo | < a => |x − (−2)| < 4
teraz idziemy w lewo i w prawo o a jednostek, w tym wypadku a = 4 i szukamy punktów odległych
mniej niż o 4 jednostki od xo
b)
| x + 2 | < 4 => znajdujemy miejsce zerowe xo = −2 bo | x − xo | < a => |x − (−2)| < 4
teraz idziemy w lewo i w prawo o a jednostek, w tym wypadku a = 4 i szukamy punktów odległych
mniej niż o 4 jednostki od xo
 => "<" −> "∧"
=> "<" −> "∧"
 Teraz tak ogólnie zapisane:
1.
|x − xo| = a
2.
|x − xo| < a
3.
|x − xo| > a
Zapamiętaj
|x − xo| < 0 − sprzeczność bo |x| ≥ 0
|x − xo| > −1 −> x∊R bo |x| ≥ 0
Teraz tak ogólnie zapisane:
1.
|x − xo| = a
2.
|x − xo| < a
3.
|x − xo| > a
Zapamiętaj
|x − xo| < 0 − sprzeczność bo |x| ≥ 0
|x − xo| > −1 −> x∊R bo |x| ≥ 0
