. qwe: Oblicz promień okręgu wpisanego w trójkąt: a)równoboczny o boku a=4 b)prostokątny równoramienny, którego wysokość opuszczona na przeciwprostokątną ma długość 3. c)o bokach a=5, b=12, c=13 Bardzo proszę o rozwiązanie tego zadanka. Byłbym bardzo wdzięczny

Bogdan: A co sam w tej sprawie ustaliłeś?, może doszukałeś się gdzieś wzorów na długość promienia okręgu wpisanego w trójkąt równoboczny, prostokątny?

Eta:

qwe:

	1		a√3
No doszukałem sie doszukałem r=		h Obliczamy chyba wysokość z wzoru h=		, a
	3		2

poźniej promień z tego. Tak? Ale to jest tak ze ja zawsze cos zawale i mi nie wyjdzie. A widząc gotowe rozwiązanie uczę się na ich podstawie. Dlatego jak coś nie wiem to proszę o całe rozwiązanie

Bogdan: Długość promienia okręgu wpisanego w trójkąt równoboczny o boku długości a

	1
wyraża się wzorem: r =		a√3.
	6

Długość promienia okręgu wpisanego w trójkąt prostokątny o przyprostokątnych

	1
długości a, b i przeciwprostokątnej długości c wynosi: r =		(a + b − c).
	2

Skorzystaj z tych wzorów i pokaż swoje rozwiązanie.

qwe: No wyszło mi tak:

	2√3
a) r=
	3

b) Tego nie wiem jak obliczyć c) r=2 Dobrze te dwa?

Kejt: jeśli ufać wzorom podanym przez Bogdana, to jest dobrze. ;>

qwe: A podpunkt B? Bo nie wiem jak to rozwiązać

qwe: Aha i jeszcze jak udowodnić, że trójkąt w podpunkcie C jest trójkątem prostokątnym?

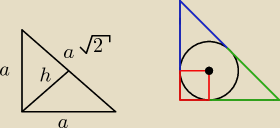
Godzio: do 2 :

h*a√2		a2
	=
2		2

a = ...

	2a − a√2
r =
	2

Jeśli czegoś nie wiesz to sie zastanów

Godzio: 5² + 12² = 13² 169 = 169 − trójkat jest prostokątny

qwe: b)

3*a√2		3√2
	⇒ a=
2		2

	2*3√22−3√22√2
r=		= 3√2−3
	2

Może być tak?

qwe: Dobrze to jest zrobione?

Godzio: 3a√2 = a² 3√2 = a r wyliczone ok ale a chyba literówka

qwe: Ok. Wielkie dzięki wszystkim za fatygę. chyba już wszystko rozumiem