Fisieeenka: Nie rozumiem zbytnio zadanka.. A raczej jego drugiej części. Jak ten wykres mam narysować.? Oblicz: f(−3), f(−2), f(−1), f(0), f(1), f(2), f(3). Na podstawie otrzymanych wyników naszkicuj wykres funkcji f: R→R. a). f(x)=x²−2x−1 b). f(x)=−¹₂x²+2¹₂

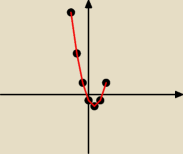
Fisieeenka: Wyniki do podpunktu a mam następujące: f(−3)=14 f(−2)=7 f(−1)=2 f(0)=−1 f(1)=−2 f(2)=−1 f(3)=2 Czy to ma wyglądać tak.?

Fisieeenka: O co chodzi w tym f: R→R .? proszę o pomoc.!

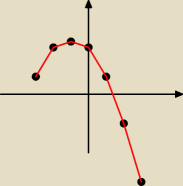
Fisieeenka: podpunkt b. f(−3)=1 f(−2)=2,5 f(−1)=3 f(0)=2,5 f(1)=1 f(2)=−1,5 f(3)=−5 tak to ma wyglądać.? Ponawiam pytanie. o co chodzi z f: R→R .?!

Gustlik: Licząc f(−3), f(−2), f(−1), f(0), f(1), f(2), f(3) podstawiasz te liczby za x do wzoru funkcji i w ten sposób otrzymasz kilka punktów leżących na paraboli i możesz teraz narysować tę parabolę. Natomiast oznaczenie f: R→R oznacza, że funkcja odwzorowuje zbiór liczb rzeczywistych w zbiór liczb rzeczywistych, czyli z polskiego na nasze: dziedziną, czyli zbiorem X jest R i zbiorem Y jest tez zbiór R, choć przy funkcji kwadratowej będzie to przedział <q, +∞) gdy a>0 lub (−∞, q> gdy a<0, q oznacza współrzędną y_w wierzchołka paraboli,

	−Δ
liczymy ją ze wzoru q=		.
	4a

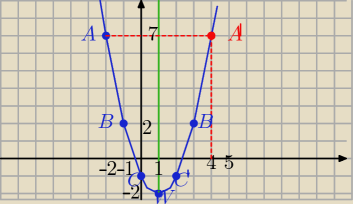
suseł: Osią symetrii paraboli jest zielona prosta : x = 1 więc punkt symetryczny do A jest A^' f( −2) = 7 = f( 4) to zaznacz na swoim rysunku f( −3) = 14 = f( 5)

suseł: Teraz na drugim rysunku zaznacz na zielono oś symetrii tej paraboli i znajź brakujace punkty symetryczne po lewej stronie i tak dokończysz rysując tę brakujacą część paraboli

suseł: Po prawej stronie "primy" przy punktach się zamazały , sorryy

Fisieeenka: dziękuję.

suseł: Rozumiesz już o co "biega" ?

Fisieeenka: no tak, tak.