 Ze sklejki w kształcie trójkąta prostokątnego wycięto koło o średnicy 8 dm. Oblicz,jaką część
pow. sklejki stanowią odpady jeżeli punkt styczności koła z najdłuższym bokiem sklejki dzieli
ten bok na odcinki mające długośći 8 dm i 12 dm .
Ze sklejki w kształcie trójkąta prostokątnego wycięto koło o średnicy 8 dm. Oblicz,jaką część
pow. sklejki stanowią odpady jeżeli punkt styczności koła z najdłuższym bokiem sklejki dzieli
ten bok na odcinki mające długośći 8 dm i 12 dm .
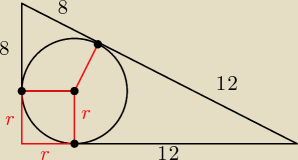 (8 + r)2 + (12 + r)2 = 202
64 + 16r + r2 + 144 + 24r + r2 = 400
2r2 + 40r − 192 = 0 /:2
r2 + 20r − 96 = 0
Δ = 400 + 384 = 784
√Δ = 28
(8 + r)2 + (12 + r)2 = 202
64 + 16r + r2 + 144 + 24r + r2 = 400
2r2 + 40r − 192 = 0 /:2
r2 + 20r − 96 = 0
Δ = 400 + 384 = 784
√Δ = 28
| −20 − 28 | ||
r1 = | = −24 − odrzucamy bo r > 0 | |
| 2 |
| −20 + 28 | ||
r2 = | = 4 | |
| 2 |
| 12 * 16 | ||
PΔ = | = 96 | |
| 2 |
 w zad, nie jest dokładnie powiedziane , jakie ma być to koło ?
myślę ,że jeżeli chodzi o "osczędność materiału"
to ma być styczne do wszystkich boków tego trójkąta
P( odpadów )= P( trójkątaa ABC) − P( koła)=........
powodzenia
w zad, nie jest dokładnie powiedziane , jakie ma być to koło ?
myślę ,że jeżeli chodzi o "osczędność materiału"
to ma być styczne do wszystkich boków tego trójkąta
P( odpadów )= P( trójkątaa ABC) − P( koła)=........
powodzenia 

 Mogłeś Godzio odrazu dodać :
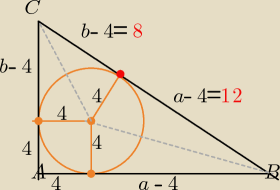
a= 12+r= 16
b= 8+r= 12
P( odpadów) = 12*12*16 − 16π= 96 − 16 π ≈........
Mogłeś Godzio odrazu dodać :
a= 12+r= 16
b= 8+r= 12
P( odpadów) = 12*12*16 − 16π= 96 − 16 π ≈........

 później ta część = 8 zobaczyłem później tą 8 i stwierdziłem że to pewnie do tej części a nie do
średnicy
później ta część = 8 zobaczyłem później tą 8 i stwierdziłem że to pewnie do tej części a nie do
średnicy
 dla mnie
dla mnie 

