MATURA 2010
xyz: TREŚCI ZADAŃ Z MATURY ROZSZERZONEJ 2010 KTÓRE PAMIĘTAMY

ZAKŁADAM WĄTEK, JAKO ŻE OBAWIAM SIĘ, ŻE POJEDYNCZE ZGINĄ W TŁUMIE BEZ ODPOWIEDZI... A TO CHYBA
FAJNE MÓC SPRAWDZIĆ SAMEGO SIEBIE.
1. Wierzchołek A trójkąta równoramiennego ma współrzędne A=(−2,5) pozostałe wierzchołki leżą na
prostej y=x+1, wiedząc, że AC=BC i pole trójkąta wynosi 15 oblicz współrzędne wie
5 maj 19:42
next: Zad 1
|2x+4| + |x −1| ≤ 9
Dobrze pamiętam?

5 maj 19:45
Svanar: nie lepiej poszukac w necie ?

5 maj 19:46
5 maj 19:47
xyz: nie Svanar, chcę dać szansę forumowiczom, żeby mogli sobie poćwiczyć oraz podyskutować na ten
temat z innymi, którzy dziś pisali. Nie zmuszam Cię do odpowiedzi. Pozdrawiam

5 maj 19:47
next: W takim razie poprawka

Zad 1 Rozwiąz nierównośc |2x+4| + |x −1| ≤ 6
5 maj 19:49
next: Zad 2.
Wyznacz wszystkie rozwiązania równania 2cos2 x − 5sin x − 4 = 0 należące do przedziału
<0, 2π> .
5 maj 19:50
tyc: jak robiliście 7

5 maj 19:53
xyz: |2x+4| + |x −1| ≤ 6
1. x∊(−
∞,−2)
−2x−4−x+1−6≤0
−3x−9≤0
x≥−3
razem: x∊<−3,−2)
2. x∊<−2,1)
2x+4−x+1−6≤0
x≤1
razem: x∊<−2,1)
3. x∊<1,
∞)
razem: x=1
odpowiedzią jest suma przedziałów z trzech przypadków czyli:
x∊<−3,1>
jeśli się nie machnęłam, bo trochę w głowie, a już dziś mózg wysiliłam

5 maj 19:53
xyz: zad 2. 2(1−sin
2x)−5snix−4=0
| | 1 | | 11 | | 7 | |
po wyliczeniu z f. kwadratowej wychodzi sinx=− |
| czyli x= |
| π v x= |
| π |
| | 2 | | 6 | | 6 | |
jesli dobrze pamiętam
5 maj 19:57
next:
xyz
Mi tak samo wyszlo

a swoją drogą ciekawy jestem tego zadania:
Zadanie 3. (4 pkt)
Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F
umieszczone tak, by |CE |= 2 DF . Oblicz wartość x = | DF | , dla której pole trójkąta AEF
jest najmniejsze.
| | 1 | |
Mi wyszło ze x = |
| móglby sie ktoś podzielić swoją odpowiedzią? |
| | 4 | |
5 maj 20:00
kalafiorowa:
| | 1 | |
moim znajomym tez wychodzilo |
| ale ja nie wiem jak do tego dzoszli  |
| | 4 | |
5 maj 20:02
Svanar: | 1 | |
| tez  |
| 4 | |
5 maj 20:02
next:
kalafiorowa
ja obliczyłem to z tego faktu że pole tego Δ wewnątrz było najmniejsze kiedy suma pól tych
czterech na zewnatrz była największa. jak wiadomo wszystkie 4 były Δ prostokątnymi więc dalej
łatwizna

5 maj 20:04
Svanar:

chyba 3

5 maj 20:06
next: ej dobra 3 zapędziłem się ale to nie zmienia faktu

5 maj 20:06
Svanar: tez tak robilem

bo boki tego w srodku to byly
√taaaaaaaaaaaakie pierwiastki
5 maj 20:07
next: tak zacząłem z tymi pierwiastkami ale jak zobaczyłem te działania od razy było wiadomo że nie o
ten sposób chodzi

5 maj 20:09
Svanar: nom.... ale ogolnie to trudna jednak byla
5 maj 20:10
next: początkowe zadania jeszcze do ogarnięcia, pożniej coraz gorzej, jak już zaczynamy to powiedzcie
jak Wam wyszło w tym
Zadanie 6. (5 pkt)
Wyznacz wszystkie wartości parametru m, dla których równanie x2 + mx + 2 = 0 ma dwa
różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od 2m2 −13 .
mi wyszedł przedział (−3, −2√2) U (2√2, 3 ) tylko nie wiem czy dobrze klamerki zapamiętałem
5 maj 20:14
xyz: no to robimy pełne rozw zad 3. i przejdziemy do następnego, żeby każdy mógł sobie orientacyjne
spraedzić

kto się podejmuje napisać zad 3?
5 maj 20:14
eee: next zad nr 6 mam tak samo

mógłby ktoś dać pełne rozw zad nr 3?
5 maj 20:19
kalafiorowa: zadanie 6 tez mam tak samo

5 maj 20:25
Svanar:
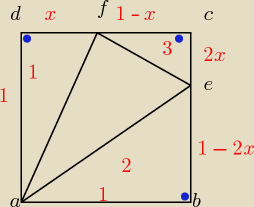
Pole trójkata AEF jest najmniejsze wtedy kiedy P
1 + P
2 + P
3 jest najwieksze
| | 1 | | 1−2x | |
P2 = |
| * (1−2x) = |
| |
| | 2 | | 2 | |
| | 1 | |
P3 = |
| * 2x * (1−x) = x−x2 |
| | 2 | |
| | x | | 1−2x | | −2x2 + x + 1 | |
P1+P2+P3 = |
| + |
| + x−x2 = |
| |
| | 2 | | 2 | | 2 | |
a=−1
5 maj 20:26
next:
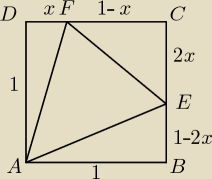
Mogę dać rysunek i treśc nie chce mi sie na razie więcej

Zadanie 3. (4 pkt)
Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F
umieszczone tak, by |CE |= 2 DF . Oblicz wartość x = | DF | , dla której pole trójkąta AEF
jest najmniejsze.
Jak mówiłem żeby pole tego Δ wewnątrz było najmniejsze suma pól tych czterech na zewnatrz musi
być największa
5 maj 20:30
Basia:
@xyz
napiszę, ale za jakąś godzinkę
połówka głodna, ja zresztą też
5 maj 20:30
suseł:
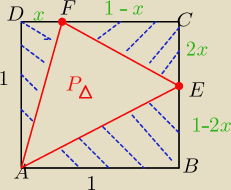
P
ΔAEF = P( kwadratu) − ( sumy pól trójkątów prostokątnych)
| | 2x*(1−x) | |
P(ECF)= |
| = x( 1−x)
|
| | 2 | |
założenie : x€(0,
12)
P(x) = 1 −
12+x −x +x
2 −
12x = x
2 −
12x +
12
P(x) −−− funkcja kwadratowa , ramiona paraboli do góry , więc osiąga minimum
| | −b | | 12 | | 1 | |
dla x= |
| = |
| = |
| spełnia założenie
|
| | 2a | | 2 | | 4 | |
odp: dla x =IDFI=
14 pole trójkąta AEF jest najmniejsze.

5 maj 20:33
xyz: ja zrobiłam tak:
zad 3.
| | 1 | | 1 | | 1 | | 1 | |
PAEF=1− |
| (1−2x)−x(1−x)− |
| x= |
| − |
| x+x2 |
| | 2 | | 2 | | 2 | | 2 | |
to co idziemy do zadania 4?
5 maj 20:35
mat: mam takie nurtujące mnie pytanko: bo napisałem w pierwszym zadaniu rozwiązanie takie:
x∊<−3,−2) znaczek sumy "n" <−2,1> a to jest przecież to samo co x∊<−3,1> uznają mi to?

5 maj 20:36
Basia:
PAEF=Pkwadratu−PADF−P{ECF}−P{ABE}
P=1*1−12[x*1+(1−x)*2x+1*(1−2x)]
P(x) = 1 − 12*[x+2x−2x2+1−2x]=
1+x2−12x−12 = x2 − 12x+12
dalej już chyba nie trzeba pisać
5 maj 20:36
next: Zad 4 wydaje się banalnie proste i chyba takie jest:
Zadanie 4. (4 pkt)
Wyznacz wartości a i b współczynników wielomianu W (x) = x3 + ax2 + bx +1 wiedząc, że
W (2) = 7 oraz, że reszta z dzielenia W (x) przez (x − 3) jest równa 10.
W(2) = 7
W(3) = 10 i po kłopocie

5 maj 20:36
Svanar: 4 to banal:
W(4) = 7
W(3) = 10
podstawic i wyliczyc
5 maj 20:36
suseł:
no w/g mnie tak

5 maj 20:37
xyz: zad4.
W(2)=7
W(3)=10
rozwiązałam taki układ i mi wyszło
5 maj 20:38
maturzysta: zadanie 7 mnie bardzo interesuje. Rozwiąże ktoś

5 maj 20:39
suseł:
zad. 4)
a= −5 b= 9

5 maj 20:39
xyz: zad 5. trochę się nad tym poplątałam ale coś wyszło

jak się nie mylę to dwie opcje
5 maj 20:39
next: Zadanie 5. (5 pkt)
O liczbach a, b, c wiemy, że ciąg (a, b, c) jest arytmetyczny i a + c =10 , zaś ciąg
(a +1, b + 4, c +19) jest geometryczny. Wyznacz te liczby.
Powstają 3 układy:
a + c = 10
a + c = 2b − z wł. ciągu aryt.
(b+4)2 = (a+1)(c+19) − z wł. ciągu geom.
Z pierwszych dwóch od razu można wyliczyć że 2b=10 czyli b = 5
5 maj 20:40
xyz: mnie też 7 najbardziej interesuje, ale czekam cierpliwie

5 maj 20:40
mat: a ja zrobiłem zad 4 tabelką Hornera hehe

czapki z głów dla tych którzy zrobili ostatnie z
ostrosłupem

5 maj 20:42
mat: w zad 7 chyba mialo wyjść (5,6) lub (−3,−2) ale nie jestem w 100% pewnien, obliczenia mi zajęły
całe 2 strony, mogłem się gdzieś walnąć...
5 maj 20:45
maturzysta: zad 7 znalazłem odpowiedz w necie ale mi się nie zgadza
odp z nata C(3,5 : 4,5) lub C( −1,5 : −0,5)
mi wyszło
C( 5, 6) lub C( −3, −2)
co wy na to


5 maj 20:45
maturzysta: ostatnie było kozackie

prawie dokończyłem zabrakło mi czasu, więc zabiorą mi 1 moze 2
punkty

5 maj 20:46
5 maj 20:49
Godzio: Może mi ktoś sprawdzić ostatnie:
5 maj 20:49
xyz: maturzysto: jak chodzi o zad 7, to mi wyszło tak jak Tobie, a mojemu facetowi, tak jak podałeś
w odpowiedziach, tzn. te niecałkowite liczby. Ja liczyłam z pola z geometrii analitycznej, on
| | 1 | |
pole z normalnego wzoru |
| ah i kto sie wypowie? |
| | 2 | |
5 maj 20:56
xyz: Godziu, a jak Ty zrobiłeś zad 7? co Ci wyszło? weźmie je ktoś zrobi?
5 maj 20:57
maturzysta: ja liczyłem z wzoru na pole trójkąta. Można było policzyć jego wysokośc bez problemu. a bok
BC=AC był, podstawą
5 maj 20:57
maturzysta: a prawdopodobieństwo jakie wam wyszło
mi 1/4
5 maj 20:58
mat: ja też pole liczyłem ze wzoru 1/2ah i mi wyszło tak jak wam.
5 maj 20:59
5 maj 21:00
xyz: maturzysto, daj proszę link do tego zad 7, które znalazłeś w necie, szukamy tam błędu

?
5 maj 21:01
mat: strona CKE padła, miała pewnie dziś więcej odwiedzin niż n−k

5 maj 21:03
xyz: a to znalazłeś to rzowiązanie zadania 7 na stronie CKE czy co?
5 maj 21:05
maturzysta: jest narazie tylko odp , nie ma rozwiazań
5 maj 21:05
maturzysta: skad wiesz że powinno wyjść 1/3 daj link
5 maj 21:06
maturzysta: ?
5 maj 21:11
mat: nie na CKE

ale mnie zdziwiło że padła,
zad 10
Kluczowa jest w tym zadaniu obserwacja, że kwadrat liczby całkowitej n może dawać tylko resztę
1 lub 0 przy dzieleniu przez 3. Rzeczywiście, jeżeli n = 3k to liczba n
2 dzieli się przez 3,
jeżeli n = 3k+ 1 to
n
2 = (3k + 1)
2 = 9k
2 + 6k + 1 = 3(3k
2 + 2k)+ 1,
więc liczba ta daje resztę 1 z dzielenia przez 3. Podobnie, jeżeli n = 3k + 2 to
n
2 = (3k + 2 )
2 = 9k
2 + 12k + 4 = 3(3k
2 + 4k + 1) + 1,
zatem znowu mamy liczbę, która przy dzieleniu przez 3 daje resztę 1.
Powyższa obserwacja oznacza, że suma kwadratów trzech liczb całkowitych dzieli się przez 3
(daje resztę 0) wtedy i tylko wtedy, gdy wszystkie 3 dzielą się przez 3 (czyli dają resztę 0),
lub gdy wszystkie 3 nie dzielą się przez 3. Tak jest, bo jedyne sumy trzech 0 i 1−ek, które
dają liczbę podzielną przez 3 to
0 + 0 + 0 = 0
1 + 1 + 1 = 3.
Możemy teraz policzyć prawdopodobieństwo. O zdarzeniach elementarnych myślimy jak o trójkach
otrzymanych oczek, czyli
|Ω | = 6
3.
Zdarzenia sprzyjające to takie, że wszystkie trzy liczby dzielą się przez 3, czyli należą do
zbioru {3,6} lub, że wszystkie 3 nie dzielą się przez 3, czyli należą do zbioru {1,2,4,5} .
Jest więc
2 ⋅2 ⋅2 + 4 ⋅4⋅4 = 8+ 64 = 72
zdarzeń sprzyjających.
Prawdopodobieństwo wynosi
72/6
3 = 6 = 1/3.
5 maj 21:12
mat: dodam tylko że to rozwiązanie nie jest mojego autorstwa

5 maj 21:12
mat: a prawidłowy wynik w zad 11 to:
V = a
3cosα / 12
√4sin2α−1
nie pytajcie o rozwiązanie bo sie przerazicie...

5 maj 21:15
xyz: wracamy do chronologii zad 6

kto się podejmuje?
5 maj 21:21
Godzio: ja moge

5 maj 21:26
Godzio:
x2 + mx + 2 = 0
zał.
Δ > 0
(x1 + x2)2 − 2x1x2 > 2m2 − 13
Δ = m2 − 8 > 0
m2 > 8
m > 2√2 v m < − 2√2
m∊(−∞,−2√2)∪(2√2,∞)
(x1 + x2)2 − 2x1x2 > 2m2 − 13
m2 − 4 > 2m2 − 13
m2 < 9
m < 3 i m > − 3
m∊(−3,3)
łącząc oba przedziały :
Odp: m∊(−3,−2√2) ∪ (2√2,3)
5 maj 21:29
Julek:
Zadanie 8
| | 1 | |
Trzeba zauważyć, że funkcja f(x) = |
|
|
| | x2 | |
| | 1 | | 1 | |
jest funkcją parzystą, czyli A = (x ; |
| ), B = (−x ; |
| )
|
| | x2 | | x2 | |
| | 1 | | | | 1 | |
P = |
| |(−x − x)( |
| ) *(−1 − |
| ) − 0| =
|
| | 2 | | | | x2 | |
| | 1 | | x2 + 1 | | 1 | | 2x2 + 2 | |
= |
| | −2x (− |
| )| = |
| | ( |
| ) |
|
| | 2 | | x2 | | 2 | | x | |
| 1 | | 2x2 + 2 | |
| | ( |
| ) | ≥ 2 / *2
|
| 2 | | x | |
4x
4 + 8x
2 + 4 − 16x
2 ≥ 0
4x
4 − 8x
2 + 4 ≥ 0
(2x
2 − 2)
2 ≥ 0
Liczba podniesiona do kwadratu, może przyjąć wartość większą lub równą zero.
Wykazane.
5 maj 21:30
mat: zad 6 prosze bardzo oto czyjeś rozwiązanie:
Sprawdźmy kiedy równanie ma dwa różne pierwiastki x1, x2 .
0 < Δ = m2 −8= (m−2√2)(m+2√2)
m∊(−∞,−2√2)u(2√2,+∞)
Korzystamy teraz ze wzorów Viète’a
x1 + x2 = −m
x1x2 = 2
Pozostało rozwiązać nierówność
x12 + x22 > 2m − 13
(x1 + x2)2 − 2x1x2 > 2m22 − 13
m2 − 4 > 2m − 13
0 > m2 − 9
0 > (m − 3)(m + 3)
m ∈ (− 3,3 ).
Odpowiedź: m ∈ (− 3,− 2√2) ∪ (2√2,3)
5 maj 21:32
mat: ciekawe ile punktów ujmą za to że nie wyrzuciłem z przedziału (−3,3)
przedziałum∊(−∞,−2√2)u(2√2,+∞) jak myślicie?
5 maj 21:39
Julek:
Zadanie 9
Zrobiłem super rysunek, aż byłem z siebie dumny, ale kliknąłem na "wyczyść"

Ogólnie to trzeba zauważyć, że
|CB| = |CG|
|AB| = |FC|
więc trójkąty były by przystające, gdyby |∠FCG| = |∠ABC|
wiemy, że
|∠BCD| = 180
o − |∠ABC|
Można stwierdzić, że
|∠BCD| + |∠BCG| + |∠FCD| + |∠FCG| = 360
o
Z tego, że EFDC i BHGC to kwadraty to :
|∠BCD| + |∠FCG| + 180
o = 360
o
|∠BCD| + |∠FCG| = 180
o
180
o − |∠ABC| + |∠FCG| = 180
o
|∠FCG| = |∠ABC|
Trójkąty te są przystające, |AC| = |FG|
5 maj 21:50
maturzysta: a zad 7

5 maj 21:53
Basia:
zadanie 11 było na forum jakieś dwa tygodnie temu, jest mniej więcej rozwiązane
poszukajcie
5 maj 22:04
5 maj 22:07
Jack: ostatni krok jest wątpliwy. Suseł wykazał związek między postacią "(a−1)(a−1)(a+1) > 0", a
tym, że "cały iloczyn jest >0". Nie dopisałeś spostrzeżenia, że a>0 (zapisałeś, że " x (...)
zawiera sie w przedziale a>0", co może nie zostać zinterpretowane na Twoją korzyść).
5 maj 22:17
Godzio:
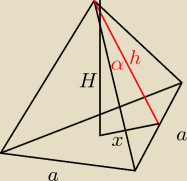 Zadanie 11
Zadanie 11
x
2 + H
2 = h
2
| | 3a2 | | a2*tg2α | |
H2 = |
| − |
| |
| | 12tg2α | | 12tg2α | |
| | a2(3 − tg2α) | | a√3−tg2α | |
H = √ |
| = |
| |
| | 2√3tgα | | 2√3tgα | |
| | 1 | | a√3−tg2α | | a2√3 | | a3√3−tg2α | |
V = |
| * |
| * |
| = |
| |
| | 3 | | 2√3tgα | | 4 | | 24tgα | |
Nie widzę żadnego błędu więc chyba w porządku

PS.
Julek 100% ?

5 maj 22:19
suseł:
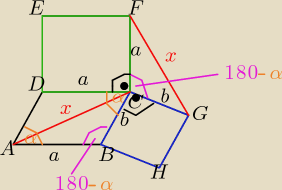
| <ABC| = |<GCF| = 180
o − α
i z tw. cosinusow:
zarówno w Δ ABC jak i w Δ GCF
x
2 = a
2+b
2 −2ab*cos(180
o− α) = a
2 +b
2 +2ab*cosα
zatem: IACI = IFGI
c.n.u

5 maj 22:26
Julek:
Niestety, ale nie

Przez całe liceum uczyłem się sam, a pod koniec klasy trzeciej wziąłem sobie korki ze
stereometrii i prawdopodobieństwa (tego nie umiałem). Akurat tych dwóch zadań z tych dwóch
działów nie zrobiłem (przynajmniej do końca)

5 maj 22:28
Julek: może za rok poprawię... nie wiem

5 maj 22:29
Jack: przyczepiłbym się do oznaczeń: nazwałeś dwa razy przez "x" odcinki, o których miałeś dowieść że
są równe... Poza tym faktycznie proste zadanie jak się zrobiło przejrzysty rysunek.
5 maj 22:32
suseł:
No dobrze: oznaczamY IACI = a
2+b
2 +2ab*cos α
i IFGI= a
2+b
2+2ab *cosα
IACI = IFGI = x ...... pasuje

5 maj 22:37
Jack: pasuje

Ta uwaga nie umniejsza Twoich zdolności w żadnym stopniu .
5 maj 22:43
suseł:

5 maj 22:51
Basia:
Witaj susełku !
A po co Ci tw.cosinusów, skoro już na rysunku pokazałaś, że
tr.GCF i tr.CBA są przystające ?
Ładnie opisać i "po ptokach"
5 maj 23:25
Basia:
@Godzio
kąt, który zaznaczyłeś nie jest kątem między sąsiednimi ścianami bocznymi
kąt między wysokościami ścian bocznych to nie to samo co kąt między ścianami
w tym tkwi błąd
szukaj w definicji kąta dwuściennego
5 maj 23:31
Basia:
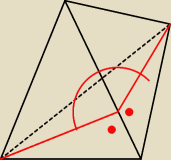
to jest kąt dwuścienny
tworzą go proste prostopadłe do krawędzi przecięcia płaszczyzn poprowadzone oczywiście przez
ten sam punkt i leżące w interesujących nas płaszczyznach
5 maj 23:36
Godzio:
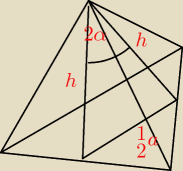
W takim razie przepraszam za błąd, Czy to o ten kąt chodzi ?
5 maj 23:43
Godzio: Jednak nie

trochę ciężko go sobie wyobrazić, ale już rozumiem

Dziękuje
5 maj 23:44
suseł:
Basiu ....to dla pewności "wszelakiej"

, mniej opisywania

Zerknij na moje rozwiązanie zda. 7

5 maj 23:45
Basia:
Ciężko, nie da się ukryć, szczególnie na rysunku. W trzech wymiarach to całkiem nieźle widać.
5 maj 23:47
Neti: Dla mnie jesteście hardcorowi że potraficie robić takie zadania. No ja jestem dopiero w II
klasie i jeszcze się waham czy zdawać podstawę czy rozszerzenie

Dla mnie osobiście zadania
1, 2, 3, 4, 6 nie są trudne a reszty jeszcze nie patrzyłam

8 maj 13:10
Patrycja: Ja powrócę jeszcze do zadania 2

Czy wynik to nie powinien być sinx=
12
16 maj 16:07
Bogdan:
Zad. 2.
2cos
x − 5sinx − 4 = 0 ⇒ 2(1 − sin
2x) − 5sinx − 4 = 0 ⇒ 2 − 2sin
2x − 5sinx − 4 = 0
2sin
2x + 5sinx + 2 = 0 i sinx ∊ <−1, 1> i x ∊ <0, 2π>
Δ = 9
| | −5 − 3 | |
sinx = |
| = −2 sprzeczność |
| | 4 | |
lub
| | −5 + 3 | | 1 | | π | | π | |
sinx = |
| = − |
| ⇒ sinx = −sin |
| ⇒ sinx = sin(− |
| ) |
| | 4 | | 2 | | 6 | | 6 | |
16 maj 16:37
Bogdan:
Poprawiam początkowy zapis: 2cos2x − 5sinx − 4 = 0
16 maj 17:05
Patrycja: No dobra mi wyszła 12 , bo nie pomnożyłam przez −1, ale gdy sinx=12 to x1= −π6,
a x2=76π
16 maj 18:07
 ZAKŁADAM WĄTEK, JAKO ŻE OBAWIAM SIĘ, ŻE POJEDYNCZE ZGINĄ W TŁUMIE BEZ ODPOWIEDZI... A TO CHYBA
FAJNE MÓC SPRAWDZIĆ SAMEGO SIEBIE.
1. Wierzchołek A trójkąta równoramiennego ma współrzędne A=(−2,5) pozostałe wierzchołki leżą na
prostej y=x+1, wiedząc, że AC=BC i pole trójkąta wynosi 15 oblicz współrzędne wie
ZAKŁADAM WĄTEK, JAKO ŻE OBAWIAM SIĘ, ŻE POJEDYNCZE ZGINĄ W TŁUMIE BEZ ODPOWIEDZI... A TO CHYBA
FAJNE MÓC SPRAWDZIĆ SAMEGO SIEBIE.
1. Wierzchołek A trójkąta równoramiennego ma współrzędne A=(−2,5) pozostałe wierzchołki leżą na
prostej y=x+1, wiedząc, że AC=BC i pole trójkąta wynosi 15 oblicz współrzędne wie



 Zad 1 Rozwiąz nierównośc |2x+4| + |x −1| ≤ 6
Zad 1 Rozwiąz nierównośc |2x+4| + |x −1| ≤ 6


 a swoją drogą ciekawy jestem tego zadania:
Zadanie 3. (4 pkt)
Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F
umieszczone tak, by |CE |= 2 DF . Oblicz wartość x = | DF | , dla której pole trójkąta AEF
jest najmniejsze.
a swoją drogą ciekawy jestem tego zadania:
Zadanie 3. (4 pkt)
Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F
umieszczone tak, by |CE |= 2 DF . Oblicz wartość x = | DF | , dla której pole trójkąta AEF
jest najmniejsze.



 chyba 3
chyba 3 

 bo boki tego w srodku to byly √taaaaaaaaaaaakie pierwiastki
bo boki tego w srodku to byly √taaaaaaaaaaaakie pierwiastki

 kto się podejmuje napisać zad 3?
kto się podejmuje napisać zad 3?
 mógłby ktoś dać pełne rozw zad nr 3?
mógłby ktoś dać pełne rozw zad nr 3?

 Pole trójkata AEF jest najmniejsze wtedy kiedy P1 + P2 + P3 jest najwieksze
Pole trójkata AEF jest najmniejsze wtedy kiedy P1 + P2 + P3 jest najwieksze
 Mogę dać rysunek i treśc nie chce mi sie na razie więcej
Mogę dać rysunek i treśc nie chce mi sie na razie więcej  Zadanie 3. (4 pkt)
Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F
umieszczone tak, by |CE |= 2 DF . Oblicz wartość x = | DF | , dla której pole trójkąta AEF
jest najmniejsze.
Jak mówiłem żeby pole tego Δ wewnątrz było najmniejsze suma pól tych czterech na zewnatrz musi
być największa
Zadanie 3. (4 pkt)
Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F
umieszczone tak, by |CE |= 2 DF . Oblicz wartość x = | DF | , dla której pole trójkąta AEF
jest najmniejsze.
Jak mówiłem żeby pole tego Δ wewnątrz było najmniejsze suma pól tych czterech na zewnatrz musi
być największa
 PΔAEF = P( kwadratu) − ( sumy pól trójkątów prostokątnych)
PΔAEF = P( kwadratu) − ( sumy pól trójkątów prostokątnych)






 jak się nie mylę to dwie opcje
jak się nie mylę to dwie opcje

 czapki z głów dla tych którzy zrobili ostatnie z
ostrosłupem
czapki z głów dla tych którzy zrobili ostatnie z
ostrosłupem


 prawie dokończyłem zabrakło mi czasu, więc zabiorą mi 1 moze 2
punkty
prawie dokończyłem zabrakło mi czasu, więc zabiorą mi 1 moze 2
punkty
 https://matematykaszkolna.pl/strona/992.html
ja nie zrobiłem 7 i 2
https://matematykaszkolna.pl/strona/992.html
ja nie zrobiłem 7 i 2  zapomniałem jak to kurcze zaczac z ta trygonometri
zapomniałem jak to kurcze zaczac z ta trygonometri



 ?
?

 ale mnie zdziwiło że padła,
zad 10
Kluczowa jest w tym zadaniu obserwacja, że kwadrat liczby całkowitej n może dawać tylko resztę
1 lub 0 przy dzieleniu przez 3. Rzeczywiście, jeżeli n = 3k to liczba n2 dzieli się przez 3,
jeżeli n = 3k+ 1 to
n2 = (3k + 1)2 = 9k2 + 6k + 1 = 3(3k2 + 2k)+ 1,
więc liczba ta daje resztę 1 z dzielenia przez 3. Podobnie, jeżeli n = 3k + 2 to
n2 = (3k + 2 )2 = 9k2 + 12k + 4 = 3(3k2 + 4k + 1) + 1,
zatem znowu mamy liczbę, która przy dzieleniu przez 3 daje resztę 1.
Powyższa obserwacja oznacza, że suma kwadratów trzech liczb całkowitych dzieli się przez 3
(daje resztę 0) wtedy i tylko wtedy, gdy wszystkie 3 dzielą się przez 3 (czyli dają resztę 0),
lub gdy wszystkie 3 nie dzielą się przez 3. Tak jest, bo jedyne sumy trzech 0 i 1−ek, które
dają liczbę podzielną przez 3 to
0 + 0 + 0 = 0
1 + 1 + 1 = 3.
Możemy teraz policzyć prawdopodobieństwo. O zdarzeniach elementarnych myślimy jak o trójkach
otrzymanych oczek, czyli
|Ω | = 63.
Zdarzenia sprzyjające to takie, że wszystkie trzy liczby dzielą się przez 3, czyli należą do
zbioru {3,6} lub, że wszystkie 3 nie dzielą się przez 3, czyli należą do zbioru {1,2,4,5} .
Jest więc
2 ⋅2 ⋅2 + 4 ⋅4⋅4 = 8+ 64 = 72
zdarzeń sprzyjających.
Prawdopodobieństwo wynosi
72/63 = 6 = 1/3.
ale mnie zdziwiło że padła,
zad 10
Kluczowa jest w tym zadaniu obserwacja, że kwadrat liczby całkowitej n może dawać tylko resztę
1 lub 0 przy dzieleniu przez 3. Rzeczywiście, jeżeli n = 3k to liczba n2 dzieli się przez 3,
jeżeli n = 3k+ 1 to
n2 = (3k + 1)2 = 9k2 + 6k + 1 = 3(3k2 + 2k)+ 1,
więc liczba ta daje resztę 1 z dzielenia przez 3. Podobnie, jeżeli n = 3k + 2 to
n2 = (3k + 2 )2 = 9k2 + 12k + 4 = 3(3k2 + 4k + 1) + 1,
zatem znowu mamy liczbę, która przy dzieleniu przez 3 daje resztę 1.
Powyższa obserwacja oznacza, że suma kwadratów trzech liczb całkowitych dzieli się przez 3
(daje resztę 0) wtedy i tylko wtedy, gdy wszystkie 3 dzielą się przez 3 (czyli dają resztę 0),
lub gdy wszystkie 3 nie dzielą się przez 3. Tak jest, bo jedyne sumy trzech 0 i 1−ek, które
dają liczbę podzielną przez 3 to
0 + 0 + 0 = 0
1 + 1 + 1 = 3.
Możemy teraz policzyć prawdopodobieństwo. O zdarzeniach elementarnych myślimy jak o trójkach
otrzymanych oczek, czyli
|Ω | = 63.
Zdarzenia sprzyjające to takie, że wszystkie trzy liczby dzielą się przez 3, czyli należą do
zbioru {3,6} lub, że wszystkie 3 nie dzielą się przez 3, czyli należą do zbioru {1,2,4,5} .
Jest więc
2 ⋅2 ⋅2 + 4 ⋅4⋅4 = 8+ 64 = 72
zdarzeń sprzyjających.
Prawdopodobieństwo wynosi
72/63 = 6 = 1/3.


 kto się podejmuje?
kto się podejmuje?

 Ogólnie to trzeba zauważyć, że
|CB| = |CG|
|AB| = |FC|
więc trójkąty były by przystające, gdyby |∠FCG| = |∠ABC|
wiemy, że
|∠BCD| = 180o − |∠ABC|
Można stwierdzić, że
|∠BCD| + |∠BCG| + |∠FCD| + |∠FCG| = 360o
Z tego, że EFDC i BHGC to kwadraty to :
|∠BCD| + |∠FCG| + 180o = 360o
|∠BCD| + |∠FCG| = 180o
180o − |∠ABC| + |∠FCG| = 180o
|∠FCG| = |∠ABC|
Trójkąty te są przystające, |AC| = |FG|
Ogólnie to trzeba zauważyć, że
|CB| = |CG|
|AB| = |FC|
więc trójkąty były by przystające, gdyby |∠FCG| = |∠ABC|
wiemy, że
|∠BCD| = 180o − |∠ABC|
Można stwierdzić, że
|∠BCD| + |∠BCG| + |∠FCD| + |∠FCG| = 360o
Z tego, że EFDC i BHGC to kwadraty to :
|∠BCD| + |∠FCG| + 180o = 360o
|∠BCD| + |∠FCG| = 180o
180o − |∠ABC| + |∠FCG| = 180o
|∠FCG| = |∠ABC|
Trójkąty te są przystające, |AC| = |FG|

 Zadanie 11
Zadanie 11
 PS. Julek 100% ?
PS. Julek 100% ? 
 | <ABC| = |<GCF| = 180o − α
i z tw. cosinusow:
zarówno w Δ ABC jak i w Δ GCF
x2 = a2+b2 −2ab*cos(180o− α) = a2 +b2 +2ab*cosα
zatem: IACI = IFGI
c.n.u
| <ABC| = |<GCF| = 180o − α
i z tw. cosinusow:
zarówno w Δ ABC jak i w Δ GCF
x2 = a2+b2 −2ab*cos(180o− α) = a2 +b2 +2ab*cosα
zatem: IACI = IFGI
c.n.u

 Przez całe liceum uczyłem się sam, a pod koniec klasy trzeciej wziąłem sobie korki ze
stereometrii i prawdopodobieństwa (tego nie umiałem). Akurat tych dwóch zadań z tych dwóch
działów nie zrobiłem (przynajmniej do końca)
Przez całe liceum uczyłem się sam, a pod koniec klasy trzeciej wziąłem sobie korki ze
stereometrii i prawdopodobieństwa (tego nie umiałem). Akurat tych dwóch zadań z tych dwóch
działów nie zrobiłem (przynajmniej do końca)


 Ta uwaga nie umniejsza Twoich zdolności w żadnym stopniu .
Ta uwaga nie umniejsza Twoich zdolności w żadnym stopniu .

 to jest kąt dwuścienny
tworzą go proste prostopadłe do krawędzi przecięcia płaszczyzn poprowadzone oczywiście przez
ten sam punkt i leżące w interesujących nas płaszczyznach
to jest kąt dwuścienny
tworzą go proste prostopadłe do krawędzi przecięcia płaszczyzn poprowadzone oczywiście przez
ten sam punkt i leżące w interesujących nas płaszczyznach
 W takim razie przepraszam za błąd, Czy to o ten kąt chodzi ?
W takim razie przepraszam za błąd, Czy to o ten kąt chodzi ?
 trochę ciężko go sobie wyobrazić, ale już rozumiem
trochę ciężko go sobie wyobrazić, ale już rozumiem  Dziękuje
Dziękuje
 , mniej opisywania
, mniej opisywania  Zerknij na moje rozwiązanie zda. 7
Zerknij na moje rozwiązanie zda. 7 
 Dla mnie osobiście zadania
1, 2, 3, 4, 6 nie są trudne a reszty jeszcze nie patrzyłam
Dla mnie osobiście zadania
1, 2, 3, 4, 6 nie są trudne a reszty jeszcze nie patrzyłam
 Czy wynik to nie powinien być sinx=12
Czy wynik to nie powinien być sinx=12