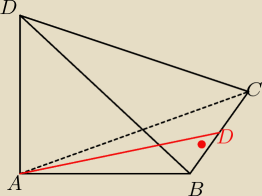
 !Podstawą ostrosłupa ABCD jest trójkąt ABC. Krawędź AD jest wysokością ostrosłupa. Oblicz
objętość ostrosłupa, jeśli wiadomo, żę AD =12, BC=6, Bd=CD=13
!Podstawą ostrosłupa ABCD jest trójkąt ABC. Krawędź AD jest wysokością ostrosłupa. Oblicz
objętość ostrosłupa, jeśli wiadomo, żę AD =12, BC=6, Bd=CD=13
 |AB|2=|BD|2−|AD|2=132−122=169−144=25
|AB|=5
△ABD i △ACD są przystające ⇒ |AC|=5
△BAC jest równoramienny ⇒
|BD|=12|BC|=3
|AD|2=|AB|2+|BD|2=52+32=25+9=34
|AD|=√34
Pp=12*6*√34 = 3√34
V=3√34*12 = 36√34
|AB|2=|BD|2−|AD|2=132−122=169−144=25
|AB|=5
△ABD i △ACD są przystające ⇒ |AC|=5
△BAC jest równoramienny ⇒
|BD|=12|BC|=3
|AD|2=|AB|2+|BD|2=52+32=25+9=34
|AD|=√34
Pp=12*6*√34 = 3√34
V=3√34*12 = 36√34
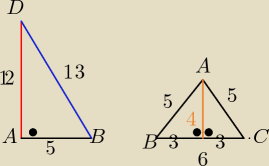 dwie ściany trójkąty prostokątne przystające ABD i ACD
z tw. Pitagorasa IABI= √169−144= √25 =5
podstawa ostrosłupa to ΔABC równoramienny
wyznaczamy hBC = √25−9= √16= 4
Pp= 12*6*4= 12
H= 12
dwie ściany trójkąty prostokątne przystające ABD i ACD
z tw. Pitagorasa IABI= √169−144= √25 =5
podstawa ostrosłupa to ΔABC równoramienny
wyznaczamy hBC = √25−9= √16= 4
Pp= 12*6*4= 12
H= 12
| 1 | ||
V= | *Pp*H= 13*12*12= 48 [ j2] | |
| 3 |





 !
!
 IADI2= IABI2 − IBDI2 = 25 −9= 16
IADI= 4
IADI2= IABI2 − IBDI2 = 25 −9= 16
IADI= 4