Ostrosłup kenia: Mamy ostrosłup prawidłowy trójkątny o krawędzi podstawy równej a. ściany boczne to trójkąty ostrokątne i kąt między sąsiednimi ścianami bocznymi ma miarę 2α. Policz objętość

kenia: zrobił to ktoś na maturze, jak to robiliście

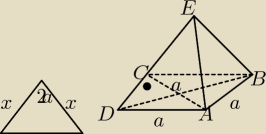
jiji: Otóż nie zdawałem w tym roku matury ale ja rozwiązałbym to w sposób następujący: skoro ostrosłup jest prawidłowy to jego ściany boczne są takie same a więc z tw.cosinusów wyznaczasz x następnie wiesz że x to wysokość opuszczona na krawędź boczną ostrosłupa czyli (1/2)ha=(1/2)rx gdzie r to długość krawędzi bocznej ostrosłupa to pierwsze równanie potem

	a2
drugie równanie z tw. pitagorasa h2+		=r2 i z układu równań wyznaczasz h−wysokość
	4

ściany bocznej a potem już z tw. pitagorasa wysokość ostrosłupa bo wiesz jak mniemam na jaki punkt została ona opuszczona i obliczenie objętości nie powinno już stanowić problemu

jiji: P.S wiem że ostrosłup jest trójkątny rysunek może niedokładny punkt C leży na krawędzi bocznej a kropka oznacza że kąt ACD jest prosty

Andy: podstawa trójkąt ...