| x | ||
tgα= | ||
| y |
| x | ||
cosα= | ||
| r |
| 5 | ||
cosα= | ||
| 13 |
| sinα | ||
tgα= | ||
| cosα |
| sinα | 5 | ||
= | |||
| cosα | 12 |
| y | ||
poprawak tgα= | ||
| x |


| 5 | ||
sinα= | cosα | |
| 12 |
| 5 | ||
( | )2cos2α+cos2α=1 | |
| 12 |
| 25 | ||
( | )2cos2α+cos2α=1 | |
| 144 |
| 169 | ||
( | )cos2α=1 | |
| 144 |
| 144 | ||
cos2α= | ||
| 169 |
| 12 | 12 | |||
cosα= | lub cosα=− | |||
| 13 | 13 |
| 25 | ||
w trzeciej liniece ma byc | cos2α+cos2α=1 | |
| 144 |
 Dzień dobry.
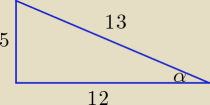
Jeśli kąt α jest ostry, to najprościej rozwiązuje się takie zadanko przez narysowanie trójkąta
prostokątnego i obliczenie długość trzeciego boku, można nawet pominąć współczynnik
proporcjonalności.
W tym przypadku przypisujemy przyprostokątnym liczby 5 i 12, (można
również wpisać 5x, 12x, ale współczynnik proporcjonalności x niczego nie wnosi do rozwiązania).
Dzień dobry.
Jeśli kąt α jest ostry, to najprościej rozwiązuje się takie zadanko przez narysowanie trójkąta
prostokątnego i obliczenie długość trzeciego boku, można nawet pominąć współczynnik
proporcjonalności.
W tym przypadku przypisujemy przyprostokątnym liczby 5 i 12, (można
również wpisać 5x, 12x, ale współczynnik proporcjonalności x niczego nie wnosi do rozwiązania).
| 12 | ||
Długość trzeciego boku = √52 + 122 = 13, cosα = | . | |
| 13 |
