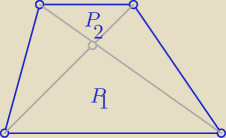
bbbb: mamy dowolny trapez i jego przekatne, ktore dziela trapez na 4 różne trójkąty. pole trojkata przy górnej podstawie trapezu wynosi 4, a przy dolnej 9. oblicz pole trapezu. wyznaczylem wzor w zaleznosci od dlugości podstaw, ale moze jest jakis sposob aby bezpośrednio policzyc pole tego trapezu?

bb: P_trapezu=(√P₁+√P₂)² P=25

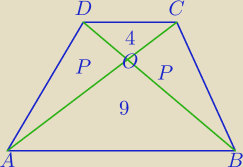
Mila: P_ΔAOD=P_ΔBOC P²=4*9 P=2*3=6 P_ABCD=4+9+2*6=25

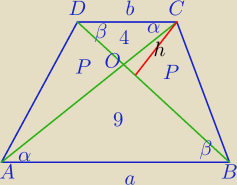
Mila: II sposób |DC|=b, |AB|=a 1) ΔDCO∼ΔABO Stosunek pól Δ podobnych jest równy kwadratowi skali podobieństwa⇔

	4		2
k2=		, ⇔k=
	9		3

2)

DO		2
	=
OB		3

PΔDOC		2		4		2
	=		⇔		=		⇔P=6
PΔCOB		3		P		3

Pole trapezu j.w.

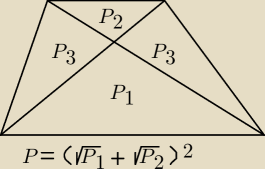
cccc: P₃ = √ P₁ P₂ pole trapezu P = (√ (P₁ + √ P₂ )²

aaaa: