Parametry m
_All: 1. Dla jakich wartości parametru m, miejsca zerowe x
1 , x
2 funkcji o wzorze
f(x)=x
2−4(m+1)x+2m(m−1) spełniają warunek x
1<m<x
2 
4 maj 19:15
_All:
4 maj 19:45
paula: omg nie pocieszaj nas takimi zadaniami...podbijam tez nie wiem o co kaman
4 maj 19:46
_All: ogolnie to nie do matury
to zwykłe zadanie domowe przygotowujące w sumie pod mature ale to
jest druga klasa ^^
Zastanawiam jak to zrobić.
Policzyłam deltę i wyszła mi taka liczba że nie mogę potem policzyć delty
m .
4 maj 19:51
paula: to chyba najpierw trzeba sprowadzic do najprostrzej postaci...wymnozyc nawiasy, potem je
opuścić itd dalej nie wiem
4 maj 19:52
_All: hehe a jeden pieron
Bez wymnażania też się da policzyć przecież
4 maj 19:59
pytajnik: podbijam
4 maj 20:10
_All: Wie ktoś?
D
4 maj 20:10
_All: 
?
4 maj 21:30
Svanar: liczysz delte (Δ>0) i "na chama" liczysz miejsca zerowe... potem przeksztalcasz
4 maj 21:32
_All: ?
4 maj 21:32
_All: aha
"na chama' Okej zobaczymy co mi z tego wyjdzie
4 maj 21:33
Godzio: nie nie nie
zaraz pokaże jak
4 maj 21:33
_All: O Godzio
Ty to zawsze uratujesz człowieka
4 maj 21:36
Godzio:
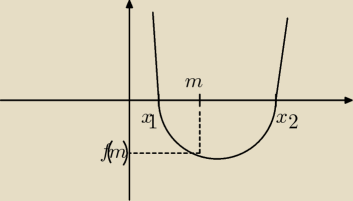
f(m) < 0
m
2 − 4(m+1)*m +2m(m−1) < 0
i to trzeba wyliczyć
4 maj 21:37
Svanar: Ty mnie teraz obrazil
4 maj 21:37
Godzio:
4 maj 21:38
_All: A takie buty ^^ Dziękuję bardzo za wskazówkę
A co powiesz do tego zadania?Jakaś wskazówka?
Udowodnij,że jeśli a, b, c, d tworzą ciąg geometryczny to
(a
2+b
2+c
2)(b
2+c
2+d
2)=(ab+bc+cd)
2
Jak się d tego zabrać?
4 maj 21:40
Svanar: ja sie teraz nie odzywam
4 maj 21:41
Godzio: przepraszam
Svanar
na pewno coś by tam wyszło gdyby dokładnie przeliczać ale po co się
męczyć
4 maj 21:41
Svanar: niech On Ci teraz powie !
4 maj 21:42
Svanar: xD
4 maj 21:42
4 maj 21:43
Svanar: ja powiem tyle....
b2 = ac
c2 = bd
4 maj 21:43
_All:
'...coś by tam wyszło...'
coś napewno
4 maj 21:44
_All: O i już prawie wszystko jasne
DZIĘKUJĘ
!
4 maj 21:44
Godzio:
b = a*q
c = a*q
2
d = a*q
3
po podstawiaj to powinno wyjść
4 maj 21:45
Godzio:
L = (a2 + a2q2 + a2q4)(a2q2 + a2q4 + a2q6) = a4q2(1 + q2 + q2)(1 + q2 + q2)
P = (a2q + a2q3 + a2q5)(a2q + a2q3 + a2q5) = a4q2(1 + q2 + q4)(1 + q2 + q4)
L = P
Jak czegoś nie rozumiesz pisz
4 maj 21:55
Godzio: chochlik się wdarł
L = (a
2 + a
2q
2 + a
2q
4)(a
2q
2 + a
2q
4 + a
2q
6) = a
4q
2(1 + q
2 + q
2)(1 + q
2 + q
4)
4 maj 21:56
_All: Rozumiem Rozumiem wszystko tylko nie wiedziałam jak do tego zabrać
dziękuję
Ale jeszcze jedno zadanie mnie męczy zanim pójdę spać to musze też zrobić
Dla jakich wartości parametru m równanie |x
2−4|=m
2+1 ma dwa różne rozwiązania?
Jak to zrobić? Może tak
1* x
2−4−1=m
2
2* −x
2+4−1=m
2
i narysować wykres z obu przypadków po dwa wykresy i odczytać w jakich przedziałach są dwa
rozwiązania czy jakoś prościej można
4 maj 22:03
