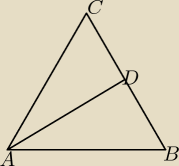
 punkt D lezy na boku BC trójkata równoramiennego ABC w którym Ac=BC. Odcinek AD dzieli triojkąt
ABC na dwa trójkąty równoramienne w taki sposób ze AD=CD oraz AB=BD. Udowodnij, że ∡ADC=5*∡ACD
punkt D lezy na boku BC trójkata równoramiennego ABC w którym Ac=BC. Odcinek AD dzieli triojkąt
ABC na dwa trójkąty równoramienne w taki sposób ze AD=CD oraz AB=BD. Udowodnij, że ∡ADC=5*∡ACD
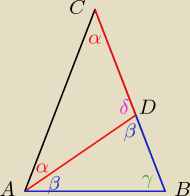 teza: δ = 5α
a dalej to juz nie idzie...
2a + δ = 180
δ + β = 180
α + β = γ
2β + γ = 180
2γ + α = 180
teza: δ = 5α
a dalej to juz nie idzie...
2a + δ = 180
δ + β = 180
α + β = γ
2β + γ = 180
2γ + α = 180