Twierdzenie talesa w zadaniu... POMÓŻCIE, prosze... Natasha : Trapez o ramionach długości 6 i 10 jest opisany na okręgu. Odcinek łączący środki ramion trapezu dzieli trapez na 2 części których pola pozostają w stosunku 3:5. Oblicz długości podstaw trapezu. Znalazłam rozwiązanie na internecie, ale jednej kwestii nei rozumiem, mianowicie :

	(8+b)*h)
P1=
	2

	(8+a)*h)
P2=
	2

Z twierdzenia Talesa wysokości górnego trapezu i dolnego są sobie równe Mógłby ktoś pomóc, pokazać to twierdzenie talesa z którego to wynika Prosze...

Natasha : ... ? Nie zapomnijcie o mnie,

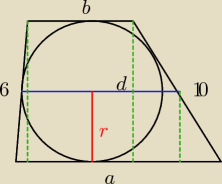
Rumpfy: a + b = 6 + 10

	a + b
d =
	2

	3P2
P1 =
	5

P₁ = {b+d}{2} * r P₂ = {a+d}{2} * r

	3(a+d)
{a+d}{2} * r =		* r
	10

cdn.

Rumpfy: ajj wszystko zle, zrobie od nowa

Rumpfy:

	b+d
P1 =		* r
	2

	a+d
P2 =		* r
	2

	a+d		3(a + d)
Pcalkowite =		* r +		* r
	2		10

a+b		a+d		3(a + d)
	* 2r =		* r +		* r
2		2		10

d = 8 ⇒ a = 12, b = 4

Natasha : aaa to rzeczywiście już widze bardzo się zagubiłam.. i to nawet chyba nie wynika tyle z twierdzenia talesa, co z tego że opisany jest trapez na okręgu Stokrotne dzięki ... teraz już wszystko jasne... DZIEKI JESZCZE RAZ