funkcja wymierna Maciek: Sporządź wykres fukncji f(x)=|^x−4_x−2|, a następnie korzystając z tego wykresu, wyznasz wszyskie wartości parametru k, dla których równanie f(x)=|^x−4_x−2| = k ma dwa rozwiązania, których iloczyn jest liczbą ujemną. przedstawiłem funkcję w postaci iloczynowej robiąc założenie że x∊R\{2}, stąd otrzymałem funkcję ze środka modułu w formie (x−2)(x−4), wymnożyłem i otrzymałem x²−6x+8 następnie wyliczyłem położenie wierzchołka na (3,−1), przekształciłem częściowo względem osi OX aby otrzymać wykres f(x). z tego wyszło że drugie równianie ma 2 rozwiązania dla k>1 a ich iloczyn jest ujemny kiedy jedna z nich jest ujemna, a druga dodatnia. Więc skoro f(0)=2 a funkcja jest rosnąca to iloczyn x₁ i x₂ jest ujemny dla k>2 wyszło mi więc k>2. Czy na maturze przeszło by to zadanie tak rozwiązane?

Svanar: ZLE CALE ZADANIE ZLE tutaj jest zle przedstawiłem funkcję w postaci iloczynowej robiąc założenie że x∊R\{2}, stąd otrzymałem funkcję ze środka modułu w formie (x−2)(x−4), wymnożyłem i otrzymałem x2−6x+8

Godzio:

	x−4		−2		−2
f(x) = |		| = |		+ 2| => narysuj wykres		+ 2 ( powinieneś to umieć)
	x−2		x−2		x−2

następnie dolną część wykresu odbij względem OX i myśle że dalej sobie poradzisz

Svanar: mi wychodzi +1 a nie +2

Godzio: zgadza się +1

robinka:

	−2
zgadzam się z Svanarem ma ma byc +1 zamiast +2 > f(x)=		+1
	x−2

Svanar: wkoncu cos dzis dobrze napisalem

robinka:

	−2
czyli bazowa funkcja F(x)=		> translacja o wektor [2,1]
	x

Maciek: ok, dzięki wielkie, gdyby nie wy jeszcze na maturze bym palnął coś podobnego czyli końcowy wynik to k∊(1,2)?

Svanar: niee teraz rysujesz wykres tej funkcji... czesc pod OX odbijasz wzgledem tej osi i wtedy szukasz rozwiazania

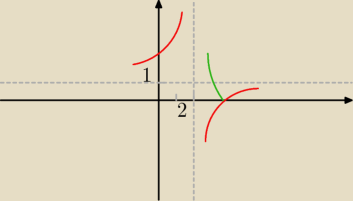
Godzio: k∊(0,1) ∪(1,∞)

Maciek: Ok, wykres już mam dobry, tylko wydaje mi się że przy k∊(0,1) ∪(1,∞) są po prostu dwa rozwiązania a tam jest: "ma dwa rozwiązania których iloczyn jest liczbą ujemną".

Godzio: a no to w takim razie k ∊ ∅

Svanar: argh dla K∊(0,1) ILOCZYN JEST DODATNI k∊(1, "punkt przeciecia z OY") xD

Maciek: Czyli tak jak mi się wydawało, bo f(0)=2 , jeszcze raz dzięki za superszybką pomoc

Svanar: np